| Cuboctahedral prism | |
|---|---|
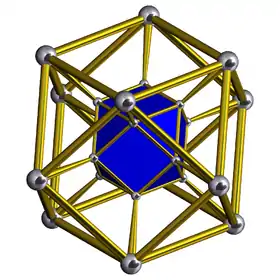 Schlegel diagram One cuboctahedral cell shown | |
| Type | Prismatic uniform 4-polytope |
| Uniform index | 50 |
| Schläfli symbol | t1,3{3,4,2} or r{3,4}×{} t0,2,3{3,3,2} or rr{3,3}×{} |
| Coxeter-Dynkin | |
| Cells | 2 (3.4.3.4) 8 (3.4.4) 6 (4.4.4) |
| Faces | 16 {3} 12+24 {4} |
| Edges | 60 |
| Vertices | 24 |
| Vertex figure | 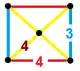 Rectangular pyramid |
| Symmetry group | [3,4,2], order 96 [3,3,2], order 48 |
| Properties | convex |
In geometry, a cuboctahedral prism is a convex uniform 4-polytope. This 4-polytope has 16 polyhedral cells: 2 cuboctahedra connected by 8 triangular prisms and 6 cubes.
It is one of 18 uniform polyhedral prisms created by using uniform prisms to connect pairs of parallel Platonic solids and Archimedean solids.
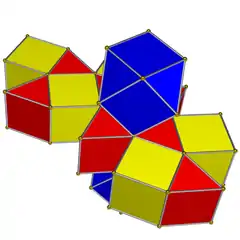 Net |
 Transparent Schlegel diagram |
Alternative names
- Cuboctahedral dyadic prism
- Rhombioctahedral prism
- Rhombioctahedral hyperprism
External links
- 6. Convex uniform prismatic polychora - Model 50, George Olshevsky.
- Klitzing, Richard. "4D uniform polytopes (polychora) x o3x4o - cope".
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.