| quarter 5-cubic honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform 5-honeycomb |
| Family | Quarter hypercubic honeycomb |
| Schläfli symbol | q{4,3,3,3,4} |
| Coxeter-Dynkin diagram | |
| 5-face type | h{4,33}, 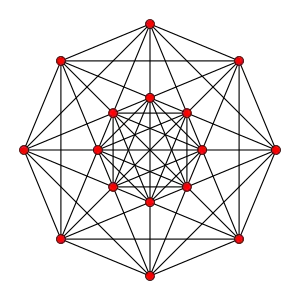 h4{4,33},  |
| Vertex figure |  Rectified 5-cell antiprism or Stretched birectified 5-simplex |
| Coxeter group | ×2 = [[31,1,3,31,1]] |
| Dual | |
| Properties | vertex-transitive |
In five-dimensional Euclidean geometry, the quarter 5-cubic honeycomb is a uniform space-filling tessellation (or honeycomb). It has half the vertices of the 5-demicubic honeycomb, and a quarter of the vertices of a 5-cube honeycomb.[1] Its facets are 5-demicubes and runcinated 5-demicubes.
Related honeycombs
This honeycomb is one of 20 uniform honeycombs constructed by the Coxeter group, all but 3 repeated in other families by extended symmetry, seen in the graph symmetry of rings in the Coxeter–Dynkin diagrams. The 20 permutations are listed with its highest extended symmetry relation:
| D5 honeycombs | |||
|---|---|---|---|
| Extended symmetry |
Extended diagram |
Extended group |
Honeycombs |
| [31,1,3,31,1] | |||
| <[31,1,3,31,1]> ↔ [31,1,3,3,4] |
↔ |
×21 = |
|
| [[31,1,3,31,1]] | ×22 | ||
| <2[31,1,3,31,1]> ↔ [4,3,3,3,4] |
↔ |
×41 = | |
| [<2[31,1,3,31,1]>] ↔ [[4,3,3,3,4]] |
↔ |
×8 = ×2 | |
See also
Regular and uniform honeycombs in 5-space:
Notes
- ↑ Coxeter, Regular and Semi-Regular Polytopes III, (1988), p318
References
- Kaleidoscopes: Selected Writings of H. S. M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- Klitzing, Richard. "5D Euclidean tesselations#5D". x3o3o x3o3o *b3*e - spaquinoh
| Space | Family | / / | ||||
|---|---|---|---|---|---|---|
| E2 | Uniform tiling | {3[3]} | δ3 | hδ3 | qδ3 | Hexagonal |
| E3 | Uniform convex honeycomb | {3[4]} | δ4 | hδ4 | qδ4 | |
| E4 | Uniform 4-honeycomb | {3[5]} | δ5 | hδ5 | qδ5 | 24-cell honeycomb |
| E5 | Uniform 5-honeycomb | {3[6]} | δ6 | hδ6 | qδ6 | |
| E6 | Uniform 6-honeycomb | {3[7]} | δ7 | hδ7 | qδ7 | 222 |
| E7 | Uniform 7-honeycomb | {3[8]} | δ8 | hδ8 | qδ8 | 133 • 331 |
| E8 | Uniform 8-honeycomb | {3[9]} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| E9 | Uniform 9-honeycomb | {3[10]} | δ10 | hδ10 | qδ10 | |
| E10 | Uniform 10-honeycomb | {3[11]} | δ11 | hδ11 | qδ11 | |
| En-1 | Uniform (n-1)-honeycomb | {3[n]} | δn | hδn | qδn | 1k2 • 2k1 • k21 |
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.