 8-simplex |
 Rectified 8-simplex |
 Truncated 8-simplex | |||||||||
 Cantellated 8-simplex |
 Runcinated 8-simplex |
 Stericated 8-simplex | |||||||||
 Pentellated 8-simplex |
 Hexicated 8-simplex |
 Heptellated 8-simplex | |||||||||
 8-orthoplex |
 Rectified 8-orthoplex |
 Truncated 8-orthoplex | |||||||||
 Cantellated 8-orthoplex |
 Runcinated 8-orthoplex | ||||||||||
 Hexicated 8-orthoplex |
 Cantellated 8-cube | ||||||||||
 Runcinated 8-cube |
 Stericated 8-cube |
 Pentellated 8-cube | |||||||||
 Hexicated 8-cube |
 Heptellated 8-cube | ||||||||||
 8-cube |
 Rectified 8-cube |
 Truncated 8-cube | |||||||||
 8-demicube |
 Truncated 8-demicube |
 Cantellated 8-demicube | |||||||||
 Runcinated 8-demicube |
 Stericated 8-demicube | ||||||||||
 Pentellated 8-demicube |
 Hexicated 8-demicube | ||||||||||
 421 |
 142 |
 241 | |||||||||
In eight-dimensional geometry, an eight-dimensional polytope or 8-polytope is a polytope contained by 7-polytope facets. Each 6-polytope ridge being shared by exactly two 7-polytope facets.
A uniform 8-polytope is one which is vertex-transitive, and constructed from uniform 7-polytope facets.
Regular 8-polytopes
Regular 8-polytopes can be represented by the Schläfli symbol {p,q,r,s,t,u,v}, with v {p,q,r,s,t,u} 7-polytope facets around each peak.
There are exactly three such convex regular 8-polytopes:
- {3,3,3,3,3,3,3} - 8-simplex
- {4,3,3,3,3,3,3} - 8-cube
- {3,3,3,3,3,3,4} - 8-orthoplex
There are no nonconvex regular 8-polytopes.
Characteristics
The topology of any given 8-polytope is defined by its Betti numbers and torsion coefficients.[1]
The value of the Euler characteristic used to characterise polyhedra does not generalize usefully to higher dimensions, and is zero for all 8-polytopes, whatever their underlying topology. This inadequacy of the Euler characteristic to reliably distinguish between different topologies in higher dimensions led to the discovery of the more sophisticated Betti numbers.[1]
Similarly, the notion of orientability of a polyhedron is insufficient to characterise the surface twistings of toroidal polytopes, and this led to the use of torsion coefficients.[1]
Uniform 8-polytopes by fundamental Coxeter groups
Uniform 8-polytopes with reflective symmetry can be generated by these four Coxeter groups, represented by permutations of rings of the Coxeter-Dynkin diagrams:
| # | Coxeter group | Forms | ||
|---|---|---|---|---|
| 1 | A8 | [37] | 135 | |
| 2 | BC8 | [4,36] | 255 | |
| 3 | D8 | [35,1,1] | 191 (64 unique) | |
| 4 | E8 | [34,2,1] | 255 | |
Selected regular and uniform 8-polytopes from each family include:
- Simplex family: A8 [37] -















- 135 uniform 8-polytopes as permutations of rings in the group diagram, including one regular:
- {37} - 8-simplex or ennea-9-tope or enneazetton -















- {37} - 8-simplex or ennea-9-tope or enneazetton -
- 135 uniform 8-polytopes as permutations of rings in the group diagram, including one regular:
- Hypercube/orthoplex family: B8 [4,36] -















- 255 uniform 8-polytopes as permutations of rings in the group diagram, including two regular ones:
- {4,36} - 8-cube or octeract-















- {36,4} - 8-orthoplex or octacross -















- {4,36} - 8-cube or octeract-
- 255 uniform 8-polytopes as permutations of rings in the group diagram, including two regular ones:
- Demihypercube D8 family: [35,1,1] -












- 191 uniform 8-polytopes as permutations of rings in the group diagram, including:
- {3,35,1} - 8-demicube or demiocteract, 151 -










 ; also as h{4,36}
; also as h{4,36} 













 .
. - {3,3,3,3,3,31,1} - 8-orthoplex, 511 -











- {3,35,1} - 8-demicube or demiocteract, 151 -
- 191 uniform 8-polytopes as permutations of rings in the group diagram, including:
- E-polytope family E8 family: [34,1,1] -












- 255 uniform 8-polytopes as permutations of rings in the group diagram, including:
- {3,3,3,3,32,1} - Thorold Gosset's semiregular 421,











- {3,34,2} - the uniform 142,











 ,
, - {3,3,34,1} - the uniform 241,











- {3,3,3,3,32,1} - Thorold Gosset's semiregular 421,
- 255 uniform 8-polytopes as permutations of rings in the group diagram, including:
Uniform prismatic forms
There are many uniform prismatic families, including:
| Uniform 8-polytope prism families | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| # | Coxeter group | Coxeter-Dynkin diagram | |||||||||
| 7+1 | |||||||||||
| 1 | A7A1 | [3,3,3,3,3,3]×[ ] | |||||||||
| 2 | B7A1 | [4,3,3,3,3,3]×[ ] | |||||||||
| 3 | D7A1 | [34,1,1]×[ ] | |||||||||
| 4 | E7A1 | [33,2,1]×[ ] | |||||||||
| 6+2 | |||||||||||
| 1 | A6I2(p) | [3,3,3,3,3]×[p] | |||||||||
| 2 | B6I2(p) | [4,3,3,3,3]×[p] | |||||||||
| 3 | D6I2(p) | [33,1,1]×[p] | |||||||||
| 4 | E6I2(p) | [3,3,3,3,3]×[p] | |||||||||
| 6+1+1 | |||||||||||
| 1 | A6A1A1 | [3,3,3,3,3]×[ ]x[ ] | |||||||||
| 2 | B6A1A1 | [4,3,3,3,3]×[ ]x[ ] | |||||||||
| 3 | D6A1A1 | [33,1,1]×[ ]x[ ] | |||||||||
| 4 | E6A1A1 | [3,3,3,3,3]×[ ]x[ ] | |||||||||
| 5+3 | |||||||||||
| 1 | A5A3 | [34]×[3,3] | |||||||||
| 2 | B5A3 | [4,33]×[3,3] | |||||||||
| 3 | D5A3 | [32,1,1]×[3,3] | |||||||||
| 4 | A5B3 | [34]×[4,3] | |||||||||
| 5 | B5B3 | [4,33]×[4,3] | |||||||||
| 6 | D5B3 | [32,1,1]×[4,3] | |||||||||
| 7 | A5H3 | [34]×[5,3] | |||||||||
| 8 | B5H3 | [4,33]×[5,3] | |||||||||
| 9 | D5H3 | [32,1,1]×[5,3] | |||||||||
| 5+2+1 | |||||||||||
| 1 | A5I2(p)A1 | [3,3,3]×[p]×[ ] | |||||||||
| 2 | B5I2(p)A1 | [4,3,3]×[p]×[ ] | |||||||||
| 3 | D5I2(p)A1 | [32,1,1]×[p]×[ ] | |||||||||
| 5+1+1+1 | |||||||||||
| 1 | A5A1A1A1 | [3,3,3]×[ ]×[ ]×[ ] | |||||||||
| 2 | B5A1A1A1 | [4,3,3]×[ ]×[ ]×[ ] | |||||||||
| 3 | D5A1A1A1 | [32,1,1]×[ ]×[ ]×[ ] | |||||||||
| 4+4 | |||||||||||
| 1 | A4A4 | [3,3,3]×[3,3,3] | |||||||||
| 2 | B4A4 | [4,3,3]×[3,3,3] | |||||||||
| 3 | D4A4 | [31,1,1]×[3,3,3] | |||||||||
| 4 | F4A4 | [3,4,3]×[3,3,3] | |||||||||
| 5 | H4A4 | [5,3,3]×[3,3,3] | |||||||||
| 6 | B4B4 | [4,3,3]×[4,3,3] | |||||||||
| 7 | D4B4 | [31,1,1]×[4,3,3] | |||||||||
| 8 | F4B4 | [3,4,3]×[4,3,3] | |||||||||
| 9 | H4B4 | [5,3,3]×[4,3,3] | |||||||||
| 10 | D4D4 | [31,1,1]×[31,1,1] | |||||||||
| 11 | F4D4 | [3,4,3]×[31,1,1] | |||||||||
| 12 | H4D4 | [5,3,3]×[31,1,1] | |||||||||
| 13 | F4×F4 | [3,4,3]×[3,4,3] | |||||||||
| 14 | H4×F4 | [5,3,3]×[3,4,3] | |||||||||
| 15 | H4H4 | [5,3,3]×[5,3,3] | |||||||||
| 4+3+1 | |||||||||||
| 1 | A4A3A1 | [3,3,3]×[3,3]×[ ] | |||||||||
| 2 | A4B3A1 | [3,3,3]×[4,3]×[ ] | |||||||||
| 3 | A4H3A1 | [3,3,3]×[5,3]×[ ] | |||||||||
| 4 | B4A3A1 | [4,3,3]×[3,3]×[ ] | |||||||||
| 5 | B4B3A1 | [4,3,3]×[4,3]×[ ] | |||||||||
| 6 | B4H3A1 | [4,3,3]×[5,3]×[ ] | |||||||||
| 7 | H4A3A1 | [5,3,3]×[3,3]×[ ] | |||||||||
| 8 | H4B3A1 | [5,3,3]×[4,3]×[ ] | |||||||||
| 9 | H4H3A1 | [5,3,3]×[5,3]×[ ] | |||||||||
| 10 | F4A3A1 | [3,4,3]×[3,3]×[ ] | |||||||||
| 11 | F4B3A1 | [3,4,3]×[4,3]×[ ] | |||||||||
| 12 | F4H3A1 | [3,4,3]×[5,3]×[ ] | |||||||||
| 13 | D4A3A1 | [31,1,1]×[3,3]×[ ] | |||||||||
| 14 | D4B3A1 | [31,1,1]×[4,3]×[ ] | |||||||||
| 15 | D4H3A1 | [31,1,1]×[5,3]×[ ] | |||||||||
| 4+2+2 | |||||||||||
| ... | |||||||||||
| 4+2+1+1 | |||||||||||
| ... | |||||||||||
| 4+1+1+1+1 | |||||||||||
| ... | |||||||||||
| 3+3+2 | |||||||||||
| 1 | A3A3I2(p) | [3,3]×[3,3]×[p] | |||||||||
| 2 | B3A3I2(p) | [4,3]×[3,3]×[p] | |||||||||
| 3 | H3A3I2(p) | [5,3]×[3,3]×[p] | |||||||||
| 4 | B3B3I2(p) | [4,3]×[4,3]×[p] | |||||||||
| 5 | H3B3I2(p) | [5,3]×[4,3]×[p] | |||||||||
| 6 | H3H3I2(p) | [5,3]×[5,3]×[p] | |||||||||
| 3+3+1+1 | |||||||||||
| 1 | A32A12 | [3,3]×[3,3]×[ ]×[ ] | |||||||||
| 2 | B3A3A12 | [4,3]×[3,3]×[ ]×[ ] | |||||||||
| 3 | H3A3A12 | [5,3]×[3,3]×[ ]×[ ] | |||||||||
| 4 | B3B3A12 | [4,3]×[4,3]×[ ]×[ ] | |||||||||
| 5 | H3B3A12 | [5,3]×[4,3]×[ ]×[ ] | |||||||||
| 6 | H3H3A12 | [5,3]×[5,3]×[ ]×[ ] | |||||||||
| 3+2+2+1 | |||||||||||
| 1 | A3I2(p)I2(q)A1 | [3,3]×[p]×[q]×[ ] | |||||||||
| 2 | B3I2(p)I2(q)A1 | [4,3]×[p]×[q]×[ ] | |||||||||
| 3 | H3I2(p)I2(q)A1 | [5,3]×[p]×[q]×[ ] | |||||||||
| 3+2+1+1+1 | |||||||||||
| 1 | A3I2(p)A13 | [3,3]×[p]×[ ]x[ ]×[ ] | |||||||||
| 2 | B3I2(p)A13 | [4,3]×[p]×[ ]x[ ]×[ ] | |||||||||
| 3 | H3I2(p)A13 | [5,3]×[p]×[ ]x[ ]×[ ] | |||||||||
| 3+1+1+1+1+1 | |||||||||||
| 1 | A3A15 | [3,3]×[ ]x[ ]×[ ]x[ ]×[ ] | |||||||||
| 2 | B3A15 | [4,3]×[ ]x[ ]×[ ]x[ ]×[ ] | |||||||||
| 3 | H3A15 | [5,3]×[ ]x[ ]×[ ]x[ ]×[ ] | |||||||||
| 2+2+2+2 | |||||||||||
| 1 | I2(p)I2(q)I2(r)I2(s) | [p]×[q]×[r]×[s] | |||||||||
| 2+2+2+1+1 | |||||||||||
| 1 | I2(p)I2(q)I2(r)A12 | [p]×[q]×[r]×[ ]×[ ] | |||||||||
| 2+2+1+1+1+1 | |||||||||||
| 2 | I2(p)I2(q)A14 | [p]×[q]×[ ]×[ ]×[ ]×[ ] | |||||||||
| 2+1+1+1+1+1+1 | |||||||||||
| 1 | I2(p)A16 | [p]×[ ]×[ ]×[ ]×[ ]×[ ]×[ ] | |||||||||
| 1+1+1+1+1+1+1+1 | |||||||||||
| 1 | A18 | [ ]×[ ]×[ ]×[ ]×[ ]×[ ]×[ ]×[ ] | |||||||||
The A8 family
The A8 family has symmetry of order 362880 (9 factorial).
There are 135 forms based on all permutations of the Coxeter-Dynkin diagrams with one or more rings. (128+8-1 cases) These are all enumerated below. Bowers-style acronym names are given in parentheses for cross-referencing.
See also a list of 8-simplex polytopes for symmetric Coxeter plane graphs of these polytopes.
| A8 uniform polytopes | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # | Coxeter-Dynkin diagram | Truncation indices |
Johnson name | Basepoint | Element counts | |||||||
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | |||||
| 1 |
|
t0 | 8-simplex (ene) | (0,0,0,0,0,0,0,0,1) | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 |
| 2 |
|
t1 | Rectified 8-simplex (rene) | (0,0,0,0,0,0,0,1,1) | 18 | 108 | 336 | 630 | 576 | 588 | 252 | 36 |
| 3 |
|
t2 | Birectified 8-simplex (bene) | (0,0,0,0,0,0,1,1,1) | 18 | 144 | 588 | 1386 | 2016 | 1764 | 756 | 84 |
| 4 |
|
t3 | Trirectified 8-simplex (trene) | (0,0,0,0,0,1,1,1,1) | 1260 | 126 | ||||||
| 5 |
|
t0,1 | Truncated 8-simplex (tene) | (0,0,0,0,0,0,0,1,2) | 288 | 72 | ||||||
| 6 |
|
t0,2 | Cantellated 8-simplex | (0,0,0,0,0,0,1,1,2) | 1764 | 252 | ||||||
| 7 |
|
t1,2 | Bitruncated 8-simplex | (0,0,0,0,0,0,1,2,2) | 1008 | 252 | ||||||
| 8 |
|
t0,3 | Runcinated 8-simplex | (0,0,0,0,0,1,1,1,2) | 4536 | 504 | ||||||
| 9 |
|
t1,3 | Bicantellated 8-simplex | (0,0,0,0,0,1,1,2,2) | 5292 | 756 | ||||||
| 10 |
|
t2,3 | Tritruncated 8-simplex | (0,0,0,0,0,1,2,2,2) | 2016 | 504 | ||||||
| 11 |
|
t0,4 | Stericated 8-simplex | (0,0,0,0,1,1,1,1,2) | 6300 | 630 | ||||||
| 12 |
|
t1,4 | Biruncinated 8-simplex | (0,0,0,0,1,1,1,2,2) | 11340 | 1260 | ||||||
| 13 |
|
t2,4 | Tricantellated 8-simplex | (0,0,0,0,1,1,2,2,2) | 8820 | 1260 | ||||||
| 14 |
|
t3,4 | Quadritruncated 8-simplex | (0,0,0,0,1,2,2,2,2) | 2520 | 630 | ||||||
| 15 |
|
t0,5 | Pentellated 8-simplex | (0,0,0,1,1,1,1,1,2) | 5040 | 504 | ||||||
| 16 |
|
t1,5 | Bistericated 8-simplex | (0,0,0,1,1,1,1,2,2) | 12600 | 1260 | ||||||
| 17 |
|
t2,5 | Triruncinated 8-simplex | (0,0,0,1,1,1,2,2,2) | 15120 | 1680 | ||||||
| 18 |
|
t0,6 | Hexicated 8-simplex | (0,0,1,1,1,1,1,1,2) | 2268 | 252 | ||||||
| 19 |
|
t1,6 | Bipentellated 8-simplex | (0,0,1,1,1,1,1,2,2) | 7560 | 756 | ||||||
| 20 |
|
t0,7 | Heptellated 8-simplex | (0,1,1,1,1,1,1,1,2) | 504 | 72 | ||||||
| 21 |
|
t0,1,2 | Cantitruncated 8-simplex | (0,0,0,0,0,0,1,2,3) | 2016 | 504 | ||||||
| 22 |
|
t0,1,3 | Runcitruncated 8-simplex | (0,0,0,0,0,1,1,2,3) | 9828 | 1512 | ||||||
| 23 |
|
t0,2,3 | Runcicantellated 8-simplex | (0,0,0,0,0,1,2,2,3) | 6804 | 1512 | ||||||
| 24 |
|
t1,2,3 | Bicantitruncated 8-simplex | (0,0,0,0,0,1,2,3,3) | 6048 | 1512 | ||||||
| 25 |
|
t0,1,4 | Steritruncated 8-simplex | (0,0,0,0,1,1,1,2,3) | 20160 | 2520 | ||||||
| 26 |
|
t0,2,4 | Stericantellated 8-simplex | (0,0,0,0,1,1,2,2,3) | 26460 | 3780 | ||||||
| 27 |
|
t1,2,4 | Biruncitruncated 8-simplex | (0,0,0,0,1,1,2,3,3) | 22680 | 3780 | ||||||
| 28 |
|
t0,3,4 | Steriruncinated 8-simplex | (0,0,0,0,1,2,2,2,3) | 12600 | 2520 | ||||||
| 29 |
|
t1,3,4 | Biruncicantellated 8-simplex | (0,0,0,0,1,2,2,3,3) | 18900 | 3780 | ||||||
| 30 |
|
t2,3,4 | Tricantitruncated 8-simplex | (0,0,0,0,1,2,3,3,3) | 10080 | 2520 | ||||||
| 31 |
|
t0,1,5 | Pentitruncated 8-simplex | (0,0,0,1,1,1,1,2,3) | 21420 | 2520 | ||||||
| 32 |
|
t0,2,5 | Penticantellated 8-simplex | (0,0,0,1,1,1,2,2,3) | 42840 | 5040 | ||||||
| 33 |
|
t1,2,5 | Bisteritruncated 8-simplex | (0,0,0,1,1,1,2,3,3) | 35280 | 5040 | ||||||
| 34 |
|
t0,3,5 | Pentiruncinated 8-simplex | (0,0,0,1,1,2,2,2,3) | 37800 | 5040 | ||||||
| 35 |
|
t1,3,5 | Bistericantellated 8-simplex | (0,0,0,1,1,2,2,3,3) | 52920 | 7560 | ||||||
| 36 |
|
t2,3,5 | Triruncitruncated 8-simplex | (0,0,0,1,1,2,3,3,3) | 27720 | 5040 | ||||||
| 37 |
|
t0,4,5 | Pentistericated 8-simplex | (0,0,0,1,2,2,2,2,3) | 13860 | 2520 | ||||||
| 38 |
|
t1,4,5 | Bisteriruncinated 8-simplex | (0,0,0,1,2,2,2,3,3) | 30240 | 5040 | ||||||
| 39 |
|
t0,1,6 | Hexitruncated 8-simplex | (0,0,1,1,1,1,1,2,3) | 12096 | 1512 | ||||||
| 40 |
|
t0,2,6 | Hexicantellated 8-simplex | (0,0,1,1,1,1,2,2,3) | 34020 | 3780 | ||||||
| 41 |
|
t1,2,6 | Bipentitruncated 8-simplex | (0,0,1,1,1,1,2,3,3) | 26460 | 3780 | ||||||
| 42 |
|
t0,3,6 | Hexiruncinated 8-simplex | (0,0,1,1,1,2,2,2,3) | 45360 | 5040 | ||||||
| 43 |
|
t1,3,6 | Bipenticantellated 8-simplex | (0,0,1,1,1,2,2,3,3) | 60480 | 7560 | ||||||
| 44 |
|
t0,4,6 | Hexistericated 8-simplex | (0,0,1,1,2,2,2,2,3) | 30240 | 3780 | ||||||
| 45 |
|
t0,5,6 | Hexipentellated 8-simplex | (0,0,1,2,2,2,2,2,3) | 9072 | 1512 | ||||||
| 46 |
|
t0,1,7 | Heptitruncated 8-simplex | (0,1,1,1,1,1,1,2,3) | 3276 | 504 | ||||||
| 47 |
|
t0,2,7 | Hepticantellated 8-simplex | (0,1,1,1,1,1,2,2,3) | 12852 | 1512 | ||||||
| 48 |
|
t0,3,7 | Heptiruncinated 8-simplex | (0,1,1,1,1,2,2,2,3) | 23940 | 2520 | ||||||
| 49 |
|
t0,1,2,3 | Runcicantitruncated 8-simplex | (0,0,0,0,0,1,2,3,4) | 12096 | 3024 | ||||||
| 50 |
|
t0,1,2,4 | Stericantitruncated 8-simplex | (0,0,0,0,1,1,2,3,4) | 45360 | 7560 | ||||||
| 51 |
|
t0,1,3,4 | Steriruncitruncated 8-simplex | (0,0,0,0,1,2,2,3,4) | 34020 | 7560 | ||||||
| 52 |
|
t0,2,3,4 | Steriruncicantellated 8-simplex | (0,0,0,0,1,2,3,3,4) | 34020 | 7560 | ||||||
| 53 |
|
t1,2,3,4 | Biruncicantitruncated 8-simplex | (0,0,0,0,1,2,3,4,4) | 30240 | 7560 | ||||||
| 54 |
|
t0,1,2,5 | Penticantitruncated 8-simplex | (0,0,0,1,1,1,2,3,4) | 70560 | 10080 | ||||||
| 55 |
|
t0,1,3,5 | Pentiruncitruncated 8-simplex | (0,0,0,1,1,2,2,3,4) | 98280 | 15120 | ||||||
| 56 |
|
t0,2,3,5 | Pentiruncicantellated 8-simplex | (0,0,0,1,1,2,3,3,4) | 90720 | 15120 | ||||||
| 57 |
|
t1,2,3,5 | Bistericantitruncated 8-simplex | (0,0,0,1,1,2,3,4,4) | 83160 | 15120 | ||||||
| 58 |
|
t0,1,4,5 | Pentisteritruncated 8-simplex | (0,0,0,1,2,2,2,3,4) | 50400 | 10080 | ||||||
| 59 |
|
t0,2,4,5 | Pentistericantellated 8-simplex | (0,0,0,1,2,2,3,3,4) | 83160 | 15120 | ||||||
| 60 |
|
t1,2,4,5 | Bisteriruncitruncated 8-simplex | (0,0,0,1,2,2,3,4,4) | 68040 | 15120 | ||||||
| 61 |
|
t0,3,4,5 | Pentisteriruncinated 8-simplex | (0,0,0,1,2,3,3,3,4) | 50400 | 10080 | ||||||
| 62 |
|
t1,3,4,5 | Bisteriruncicantellated 8-simplex | (0,0,0,1,2,3,3,4,4) | 75600 | 15120 | ||||||
| 63 |
|
t2,3,4,5 | Triruncicantitruncated 8-simplex | (0,0,0,1,2,3,4,4,4) | 40320 | 10080 | ||||||
| 64 |
|
t0,1,2,6 | Hexicantitruncated 8-simplex | (0,0,1,1,1,1,2,3,4) | 52920 | 7560 | ||||||
| 65 |
|
t0,1,3,6 | Hexiruncitruncated 8-simplex | (0,0,1,1,1,2,2,3,4) | 113400 | 15120 | ||||||
| 66 |
|
t0,2,3,6 | Hexiruncicantellated 8-simplex | (0,0,1,1,1,2,3,3,4) | 98280 | 15120 | ||||||
| 67 |
|
t1,2,3,6 | Bipenticantitruncated 8-simplex | (0,0,1,1,1,2,3,4,4) | 90720 | 15120 | ||||||
| 68 |
|
t0,1,4,6 | Hexisteritruncated 8-simplex | (0,0,1,1,2,2,2,3,4) | 105840 | 15120 | ||||||
| 69 |
|
t0,2,4,6 | Hexistericantellated 8-simplex | (0,0,1,1,2,2,3,3,4) | 158760 | 22680 | ||||||
| 70 |
|
t1,2,4,6 | Bipentiruncitruncated 8-simplex | (0,0,1,1,2,2,3,4,4) | 136080 | 22680 | ||||||
| 71 |
|
t0,3,4,6 | Hexisteriruncinated 8-simplex | (0,0,1,1,2,3,3,3,4) | 90720 | 15120 | ||||||
| 72 |
|
t1,3,4,6 | Bipentiruncicantellated 8-simplex | (0,0,1,1,2,3,3,4,4) | 136080 | 22680 | ||||||
| 73 |
|
t0,1,5,6 | Hexipentitruncated 8-simplex | (0,0,1,2,2,2,2,3,4) | 41580 | 7560 | ||||||
| 74 |
|
t0,2,5,6 | Hexipenticantellated 8-simplex | (0,0,1,2,2,2,3,3,4) | 98280 | 15120 | ||||||
| 75 |
|
t1,2,5,6 | Bipentisteritruncated 8-simplex | (0,0,1,2,2,2,3,4,4) | 75600 | 15120 | ||||||
| 76 |
|
t0,3,5,6 | Hexipentiruncinated 8-simplex | (0,0,1,2,2,3,3,3,4) | 98280 | 15120 | ||||||
| 77 |
|
t0,4,5,6 | Hexipentistericated 8-simplex | (0,0,1,2,3,3,3,3,4) | 41580 | 7560 | ||||||
| 78 |
|
t0,1,2,7 | Hepticantitruncated 8-simplex | (0,1,1,1,1,1,2,3,4) | 18144 | 3024 | ||||||
| 79 |
|
t0,1,3,7 | Heptiruncitruncated 8-simplex | (0,1,1,1,1,2,2,3,4) | 56700 | 7560 | ||||||
| 80 |
|
t0,2,3,7 | Heptiruncicantellated 8-simplex | (0,1,1,1,1,2,3,3,4) | 45360 | 7560 | ||||||
| 81 |
|
t0,1,4,7 | Heptisteritruncated 8-simplex | (0,1,1,1,2,2,2,3,4) | 80640 | 10080 | ||||||
| 82 |
|
t0,2,4,7 | Heptistericantellated 8-simplex | (0,1,1,1,2,2,3,3,4) | 113400 | 15120 | ||||||
| 83 |
|
t0,3,4,7 | Heptisteriruncinated 8-simplex | (0,1,1,1,2,3,3,3,4) | 60480 | 10080 | ||||||
| 84 |
|
t0,1,5,7 | Heptipentitruncated 8-simplex | (0,1,1,2,2,2,2,3,4) | 56700 | 7560 | ||||||
| 85 |
|
t0,2,5,7 | Heptipenticantellated 8-simplex | (0,1,1,2,2,2,3,3,4) | 120960 | 15120 | ||||||
| 86 |
|
t0,1,6,7 | Heptihexitruncated 8-simplex | (0,1,2,2,2,2,2,3,4) | 18144 | 3024 | ||||||
| 87 |
|
t0,1,2,3,4 | Steriruncicantitruncated 8-simplex | (0,0,0,0,1,2,3,4,5) | 60480 | 15120 | ||||||
| 88 |
|
t0,1,2,3,5 | Pentiruncicantitruncated 8-simplex | (0,0,0,1,1,2,3,4,5) | 166320 | 30240 | ||||||
| 89 |
|
t0,1,2,4,5 | Pentistericantitruncated 8-simplex | (0,0,0,1,2,2,3,4,5) | 136080 | 30240 | ||||||
| 90 |
|
t0,1,3,4,5 | Pentisteriruncitruncated 8-simplex | (0,0,0,1,2,3,3,4,5) | 136080 | 30240 | ||||||
| 91 |
|
t0,2,3,4,5 | Pentisteriruncicantellated 8-simplex | (0,0,0,1,2,3,4,4,5) | 136080 | 30240 | ||||||
| 92 |
|
t1,2,3,4,5 | Bisteriruncicantitruncated 8-simplex | (0,0,0,1,2,3,4,5,5) | 120960 | 30240 | ||||||
| 93 |
|
t0,1,2,3,6 | Hexiruncicantitruncated 8-simplex | (0,0,1,1,1,2,3,4,5) | 181440 | 30240 | ||||||
| 94 |
|
t0,1,2,4,6 | Hexistericantitruncated 8-simplex | (0,0,1,1,2,2,3,4,5) | 272160 | 45360 | ||||||
| 95 |
|
t0,1,3,4,6 | Hexisteriruncitruncated 8-simplex | (0,0,1,1,2,3,3,4,5) | 249480 | 45360 | ||||||
| 96 |
|
t0,2,3,4,6 | Hexisteriruncicantellated 8-simplex | (0,0,1,1,2,3,4,4,5) | 249480 | 45360 | ||||||
| 97 |
|
t1,2,3,4,6 | Bipentiruncicantitruncated 8-simplex | (0,0,1,1,2,3,4,5,5) | 226800 | 45360 | ||||||
| 98 |
|
t0,1,2,5,6 | Hexipenticantitruncated 8-simplex | (0,0,1,2,2,2,3,4,5) | 151200 | 30240 | ||||||
| 99 |
|
t0,1,3,5,6 | Hexipentiruncitruncated 8-simplex | (0,0,1,2,2,3,3,4,5) | 249480 | 45360 | ||||||
| 100 |
|
t0,2,3,5,6 | Hexipentiruncicantellated 8-simplex | (0,0,1,2,2,3,4,4,5) | 226800 | 45360 | ||||||
| 101 |
|
t1,2,3,5,6 | Bipentistericantitruncated 8-simplex | (0,0,1,2,2,3,4,5,5) | 204120 | 45360 | ||||||
| 102 |
|
t0,1,4,5,6 | Hexipentisteritruncated 8-simplex | (0,0,1,2,3,3,3,4,5) | 151200 | 30240 | ||||||
| 103 |
|
t0,2,4,5,6 | Hexipentistericantellated 8-simplex | (0,0,1,2,3,3,4,4,5) | 249480 | 45360 | ||||||
| 104 |
|
t0,3,4,5,6 | Hexipentisteriruncinated 8-simplex | (0,0,1,2,3,4,4,4,5) | 151200 | 30240 | ||||||
| 105 |
|
t0,1,2,3,7 | Heptiruncicantitruncated 8-simplex | (0,1,1,1,1,2,3,4,5) | 83160 | 15120 | ||||||
| 106 |
|
t0,1,2,4,7 | Heptistericantitruncated 8-simplex | (0,1,1,1,2,2,3,4,5) | 196560 | 30240 | ||||||
| 107 |
|
t0,1,3,4,7 | Heptisteriruncitruncated 8-simplex | (0,1,1,1,2,3,3,4,5) | 166320 | 30240 | ||||||
| 108 |
|
t0,2,3,4,7 | Heptisteriruncicantellated 8-simplex | (0,1,1,1,2,3,4,4,5) | 166320 | 30240 | ||||||
| 109 |
|
t0,1,2,5,7 | Heptipenticantitruncated 8-simplex | (0,1,1,2,2,2,3,4,5) | 196560 | 30240 | ||||||
| 110 |
|
t0,1,3,5,7 | Heptipentiruncitruncated 8-simplex | (0,1,1,2,2,3,3,4,5) | 294840 | 45360 | ||||||
| 111 |
|
t0,2,3,5,7 | Heptipentiruncicantellated 8-simplex | (0,1,1,2,2,3,4,4,5) | 272160 | 45360 | ||||||
| 112 |
|
t0,1,4,5,7 | Heptipentisteritruncated 8-simplex | (0,1,1,2,3,3,3,4,5) | 166320 | 30240 | ||||||
| 113 |
|
t0,1,2,6,7 | Heptihexicantitruncated 8-simplex | (0,1,2,2,2,2,3,4,5) | 83160 | 15120 | ||||||
| 114 |
|
t0,1,3,6,7 | Heptihexiruncitruncated 8-simplex | (0,1,2,2,2,3,3,4,5) | 196560 | 30240 | ||||||
| 115 |
|
t0,1,2,3,4,5 | Pentisteriruncicantitruncated 8-simplex | (0,0,0,1,2,3,4,5,6) | 241920 | 60480 | ||||||
| 116 |
|
t0,1,2,3,4,6 | Hexisteriruncicantitruncated 8-simplex | (0,0,1,1,2,3,4,5,6) | 453600 | 90720 | ||||||
| 117 |
|
t0,1,2,3,5,6 | Hexipentiruncicantitruncated 8-simplex | (0,0,1,2,2,3,4,5,6) | 408240 | 90720 | ||||||
| 118 |
|
t0,1,2,4,5,6 | Hexipentistericantitruncated 8-simplex | (0,0,1,2,3,3,4,5,6) | 408240 | 90720 | ||||||
| 119 |
|
t0,1,3,4,5,6 | Hexipentisteriruncitruncated 8-simplex | (0,0,1,2,3,4,4,5,6) | 408240 | 90720 | ||||||
| 120 |
|
t0,2,3,4,5,6 | Hexipentisteriruncicantellated 8-simplex | (0,0,1,2,3,4,5,5,6) | 408240 | 90720 | ||||||
| 121 |
|
t1,2,3,4,5,6 | Bipentisteriruncicantitruncated 8-simplex | (0,0,1,2,3,4,5,6,6) | 362880 | 90720 | ||||||
| 122 |
|
t0,1,2,3,4,7 | Heptisteriruncicantitruncated 8-simplex | (0,1,1,1,2,3,4,5,6) | 302400 | 60480 | ||||||
| 123 |
|
t0,1,2,3,5,7 | Heptipentiruncicantitruncated 8-simplex | (0,1,1,2,2,3,4,5,6) | 498960 | 90720 | ||||||
| 124 |
|
t0,1,2,4,5,7 | Heptipentistericantitruncated 8-simplex | (0,1,1,2,3,3,4,5,6) | 453600 | 90720 | ||||||
| 125 |
|
t0,1,3,4,5,7 | Heptipentisteriruncitruncated 8-simplex | (0,1,1,2,3,4,4,5,6) | 453600 | 90720 | ||||||
| 126 |
|
t0,2,3,4,5,7 | Heptipentisteriruncicantellated 8-simplex | (0,1,1,2,3,4,5,5,6) | 453600 | 90720 | ||||||
| 127 |
|
t0,1,2,3,6,7 | Heptihexiruncicantitruncated 8-simplex | (0,1,2,2,2,3,4,5,6) | 302400 | 60480 | ||||||
| 128 |
|
t0,1,2,4,6,7 | Heptihexistericantitruncated 8-simplex | (0,1,2,2,3,3,4,5,6) | 498960 | 90720 | ||||||
| 129 |
|
t0,1,3,4,6,7 | Heptihexisteriruncitruncated 8-simplex | (0,1,2,2,3,4,4,5,6) | 453600 | 90720 | ||||||
| 130 |
|
t0,1,2,5,6,7 | Heptihexipenticantitruncated 8-simplex | (0,1,2,3,3,3,4,5,6) | 302400 | 60480 | ||||||
| 131 |
|
t0,1,2,3,4,5,6 | Hexipentisteriruncicantitruncated 8-simplex | (0,0,1,2,3,4,5,6,7) | 725760 | 181440 | ||||||
| 132 |
|
t0,1,2,3,4,5,7 | Heptipentisteriruncicantitruncated 8-simplex | (0,1,1,2,3,4,5,6,7) | 816480 | 181440 | ||||||
| 133 |
|
t0,1,2,3,4,6,7 | Heptihexisteriruncicantitruncated 8-simplex | (0,1,2,2,3,4,5,6,7) | 816480 | 181440 | ||||||
| 134 |
|
t0,1,2,3,5,6,7 | Heptihexipentiruncicantitruncated 8-simplex | (0,1,2,3,3,4,5,6,7) | 816480 | 181440 | ||||||
| 135 |
|
t0,1,2,3,4,5,6,7 | Omnitruncated 8-simplex | (0,1,2,3,4,5,6,7,8) | 1451520 | 362880 | ||||||
The B8 family
The B8 family has symmetry of order 10321920 (8 factorial x 28). There are 255 forms based on all permutations of the Coxeter-Dynkin diagrams with one or more rings.
See also a list of B8 polytopes for symmetric Coxeter plane graphs of these polytopes.
| B8 uniform polytopes | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # | Coxeter-Dynkin diagram | Schläfli symbol |
Name | Element counts | ||||||||
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | |||||
| 1 | t0{36,4} | 8-orthoplex Diacosipentacontahexazetton (ek) | 256 | 1024 | 1792 | 1792 | 1120 | 448 | 112 | 16 | ||
| 2 | t1{36,4} | Rectified 8-orthoplex Rectified diacosipentacontahexazetton (rek) | 272 | 3072 | 8960 | 12544 | 10080 | 4928 | 1344 | 112 | ||
| 3 | t2{36,4} | Birectified 8-orthoplex Birectified diacosipentacontahexazetton (bark) | 272 | 3184 | 16128 | 34048 | 36960 | 22400 | 6720 | 448 | ||
| 4 | t3{36,4} | Trirectified 8-orthoplex Trirectified diacosipentacontahexazetton (tark) | 272 | 3184 | 16576 | 48384 | 71680 | 53760 | 17920 | 1120 | ||
| 5 | t3{4,36} | Trirectified 8-cube Trirectified octeract (tro) | 272 | 3184 | 16576 | 47712 | 80640 | 71680 | 26880 | 1792 | ||
| 6 | t2{4,36} | Birectified 8-cube Birectified octeract (bro) | 272 | 3184 | 14784 | 36960 | 55552 | 50176 | 21504 | 1792 | ||
| 7 | t1{4,36} | Rectified 8-cube Rectified octeract (recto) | 272 | 2160 | 7616 | 15456 | 19712 | 16128 | 7168 | 1024 | ||
| 8 | t0{4,36} | 8-cube Octeract (octo) | 16 | 112 | 448 | 1120 | 1792 | 1792 | 1024 | 256 | ||
| 9 | t0,1{36,4} | Truncated 8-orthoplex Truncated diacosipentacontahexazetton (tek) | 1456 | 224 | ||||||||
| 10 | t0,2{36,4} | Cantellated 8-orthoplex Small rhombated diacosipentacontahexazetton (srek) | 14784 | 1344 | ||||||||
| 11 | t1,2{36,4} | Bitruncated 8-orthoplex Bitruncated diacosipentacontahexazetton (batek) | 8064 | 1344 | ||||||||
| 12 | t0,3{36,4} | Runcinated 8-orthoplex Small prismated diacosipentacontahexazetton (spek) | 60480 | 4480 | ||||||||
| 13 | t1,3{36,4} | Bicantellated 8-orthoplex Small birhombated diacosipentacontahexazetton (sabork) | 67200 | 6720 | ||||||||
| 14 | t2,3{36,4} | Tritruncated 8-orthoplex Tritruncated diacosipentacontahexazetton (tatek) | 24640 | 4480 | ||||||||
| 15 | t0,4{36,4} | Stericated 8-orthoplex Small cellated diacosipentacontahexazetton (scak) | 125440 | 8960 | ||||||||
| 16 | t1,4{36,4} | Biruncinated 8-orthoplex Small biprismated diacosipentacontahexazetton (sabpek) | 215040 | 17920 | ||||||||
| 17 | t2,4{36,4} | Tricantellated 8-orthoplex Small trirhombated diacosipentacontahexazetton (satrek) | 161280 | 17920 | ||||||||
| 18 | t3,4{4,36} | Quadritruncated 8-cube Octeractidiacosipentacontahexazetton (oke) | 44800 | 8960 | ||||||||
| 19 | t0,5{36,4} | Pentellated 8-orthoplex Small terated diacosipentacontahexazetton (setek) | 134400 | 10752 | ||||||||
| 20 | t1,5{36,4} | Bistericated 8-orthoplex Small bicellated diacosipentacontahexazetton (sibcak) | 322560 | 26880 | ||||||||
| 21 | t2,5{4,36} | Triruncinated 8-cube Small triprismato-octeractidiacosipentacontahexazetton (sitpoke) | 376320 | 35840 | ||||||||
| 22 | t2,4{4,36} | Tricantellated 8-cube Small trirhombated octeract (satro) | 215040 | 26880 | ||||||||
| 23 | t2,3{4,36} | Tritruncated 8-cube Tritruncated octeract (tato) | 48384 | 10752 | ||||||||
| 24 | t0,6{36,4} | Hexicated 8-orthoplex Small petated diacosipentacontahexazetton (supek) | 64512 | 7168 | ||||||||
| 25 | t1,6{4,36} | Bipentellated 8-cube Small biteri-octeractidiacosipentacontahexazetton (sabtoke) | 215040 | 21504 | ||||||||
| 26 | t1,5{4,36} | Bistericated 8-cube Small bicellated octeract (sobco) | 358400 | 35840 | ||||||||
| 27 | t1,4{4,36} | Biruncinated 8-cube Small biprismated octeract (sabepo) | 322560 | 35840 | ||||||||
| 28 | t1,3{4,36} | Bicantellated 8-cube Small birhombated octeract (subro) | 150528 | 21504 | ||||||||
| 29 | t1,2{4,36} | Bitruncated 8-cube Bitruncated octeract (bato) | 28672 | 7168 | ||||||||
| 30 | t0,7{4,36} | Heptellated 8-cube Small exi-octeractidiacosipentacontahexazetton (saxoke) | 14336 | 2048 | ||||||||
| 31 | t0,6{4,36} | Hexicated 8-cube Small petated octeract (supo) | 64512 | 7168 | ||||||||
| 32 | t0,5{4,36} | Pentellated 8-cube Small terated octeract (soto) | 143360 | 14336 | ||||||||
| 33 | t0,4{4,36} | Stericated 8-cube Small cellated octeract (soco) | 179200 | 17920 | ||||||||
| 34 | t0,3{4,36} | Runcinated 8-cube Small prismated octeract (sopo) | 129024 | 14336 | ||||||||
| 35 | t0,2{4,36} | Cantellated 8-cube Small rhombated octeract (soro) | 50176 | 7168 | ||||||||
| 36 | t0,1{4,36} | Truncated 8-cube Truncated octeract (tocto) | 8192 | 2048 | ||||||||
| 37 | t0,1,2{36,4} | Cantitruncated 8-orthoplex Great rhombated diacosipentacontahexazetton | 16128 | 2688 | ||||||||
| 38 | t0,1,3{36,4} | Runcitruncated 8-orthoplex Prismatotruncated diacosipentacontahexazetton | 127680 | 13440 | ||||||||
| 39 | t0,2,3{36,4} | Runcicantellated 8-orthoplex Prismatorhombated diacosipentacontahexazetton | 80640 | 13440 | ||||||||
| 40 | t1,2,3{36,4} | Bicantitruncated 8-orthoplex Great birhombated diacosipentacontahexazetton | 73920 | 13440 | ||||||||
| 41 | t0,1,4{36,4} | Steritruncated 8-orthoplex Cellitruncated diacosipentacontahexazetton | 394240 | 35840 | ||||||||
| 42 | t0,2,4{36,4} | Stericantellated 8-orthoplex Cellirhombated diacosipentacontahexazetton | 483840 | 53760 | ||||||||
| 43 | t1,2,4{36,4} | Biruncitruncated 8-orthoplex Biprismatotruncated diacosipentacontahexazetton | 430080 | 53760 | ||||||||
| 44 | t0,3,4{36,4} | Steriruncinated 8-orthoplex Celliprismated diacosipentacontahexazetton | 215040 | 35840 | ||||||||
| 45 | t1,3,4{36,4} | Biruncicantellated 8-orthoplex Biprismatorhombated diacosipentacontahexazetton | 322560 | 53760 | ||||||||
| 46 | t2,3,4{36,4} | Tricantitruncated 8-orthoplex Great trirhombated diacosipentacontahexazetton | 179200 | 35840 | ||||||||
| 47 | t0,1,5{36,4} | Pentitruncated 8-orthoplex Teritruncated diacosipentacontahexazetton | 564480 | 53760 | ||||||||
| 48 | t0,2,5{36,4} | Penticantellated 8-orthoplex Terirhombated diacosipentacontahexazetton | 1075200 | 107520 | ||||||||
| 49 | t1,2,5{36,4} | Bisteritruncated 8-orthoplex Bicellitruncated diacosipentacontahexazetton | 913920 | 107520 | ||||||||
| 50 | t0,3,5{36,4} | Pentiruncinated 8-orthoplex Teriprismated diacosipentacontahexazetton | 913920 | 107520 | ||||||||
| 51 | t1,3,5{36,4} | Bistericantellated 8-orthoplex Bicellirhombated diacosipentacontahexazetton | 1290240 | 161280 | ||||||||
| 52 | t2,3,5{36,4} | Triruncitruncated 8-orthoplex Triprismatotruncated diacosipentacontahexazetton | 698880 | 107520 | ||||||||
| 53 | t0,4,5{36,4} | Pentistericated 8-orthoplex Tericellated diacosipentacontahexazetton | 322560 | 53760 | ||||||||
| 54 | t1,4,5{36,4} | Bisteriruncinated 8-orthoplex Bicelliprismated diacosipentacontahexazetton | 698880 | 107520 | ||||||||
| 55 | t2,3,5{4,36} | Triruncitruncated 8-cube Triprismatotruncated octeract | 645120 | 107520 | ||||||||
| 56 | t2,3,4{4,36} | Tricantitruncated 8-cube Great trirhombated octeract | 241920 | 53760 | ||||||||
| 57 | t0,1,6{36,4} | Hexitruncated 8-orthoplex Petitruncated diacosipentacontahexazetton | 344064 | 43008 | ||||||||
| 58 | t0,2,6{36,4} | Hexicantellated 8-orthoplex Petirhombated diacosipentacontahexazetton | 967680 | 107520 | ||||||||
| 59 | t1,2,6{36,4} | Bipentitruncated 8-orthoplex Biteritruncated diacosipentacontahexazetton | 752640 | 107520 | ||||||||
| 60 | t0,3,6{36,4} | Hexiruncinated 8-orthoplex Petiprismated diacosipentacontahexazetton | 1290240 | 143360 | ||||||||
| 61 | t1,3,6{36,4} | Bipenticantellated 8-orthoplex Biterirhombated diacosipentacontahexazetton | 1720320 | 215040 | ||||||||
| 62 | t1,4,5{4,36} | Bisteriruncinated 8-cube Bicelliprismated octeract | 860160 | 143360 | ||||||||
| 63 | t0,4,6{36,4} | Hexistericated 8-orthoplex Peticellated diacosipentacontahexazetton | 860160 | 107520 | ||||||||
| 64 | t1,3,6{4,36} | Bipenticantellated 8-cube Biterirhombated octeract | 1720320 | 215040 | ||||||||
| 65 | t1,3,5{4,36} | Bistericantellated 8-cube Bicellirhombated octeract | 1505280 | 215040 | ||||||||
| 66 | t1,3,4{4,36} | Biruncicantellated 8-cube Biprismatorhombated octeract | 537600 | 107520 | ||||||||
| 67 | t0,5,6{36,4} | Hexipentellated 8-orthoplex Petiterated diacosipentacontahexazetton | 258048 | 43008 | ||||||||
| 68 | t1,2,6{4,36} | Bipentitruncated 8-cube Biteritruncated octeract | 752640 | 107520 | ||||||||
| 69 | t1,2,5{4,36} | Bisteritruncated 8-cube Bicellitruncated octeract | 1003520 | 143360 | ||||||||
| 70 | t1,2,4{4,36} | Biruncitruncated 8-cube Biprismatotruncated octeract | 645120 | 107520 | ||||||||
| 71 | t1,2,3{4,36} | Bicantitruncated 8-cube Great birhombated octeract | 172032 | 43008 | ||||||||
| 72 | t0,1,7{36,4} | Heptitruncated 8-orthoplex Exitruncated diacosipentacontahexazetton | 93184 | 14336 | ||||||||
| 73 | t0,2,7{36,4} | Hepticantellated 8-orthoplex Exirhombated diacosipentacontahexazetton | 365568 | 43008 | ||||||||
| 74 | t0,5,6{4,36} | Hexipentellated 8-cube Petiterated octeract | 258048 | 43008 | ||||||||
| 75 | t0,3,7{36,4} | Heptiruncinated 8-orthoplex Exiprismated diacosipentacontahexazetton | 680960 | 71680 | ||||||||
| 76 | t0,4,6{4,36} | Hexistericated 8-cube Peticellated octeract | 860160 | 107520 | ||||||||
| 77 | t0,4,5{4,36} | Pentistericated 8-cube Tericellated octeract | 394240 | 71680 | ||||||||
| 78 | t0,3,7{4,36} | Heptiruncinated 8-cube Exiprismated octeract | 680960 | 71680 | ||||||||
| 79 | t0,3,6{4,36} | Hexiruncinated 8-cube Petiprismated octeract | 1290240 | 143360 | ||||||||
| 80 | t0,3,5{4,36} | Pentiruncinated 8-cube Teriprismated octeract | 1075200 | 143360 | ||||||||
| 81 | t0,3,4{4,36} | Steriruncinated 8-cube Celliprismated octeract | 358400 | 71680 | ||||||||
| 82 | t0,2,7{4,36} | Hepticantellated 8-cube Exirhombated octeract | 365568 | 43008 | ||||||||
| 83 | t0,2,6{4,36} | Hexicantellated 8-cube Petirhombated octeract | 967680 | 107520 | ||||||||
| 84 | t0,2,5{4,36} | Penticantellated 8-cube Terirhombated octeract | 1218560 | 143360 | ||||||||
| 85 | t0,2,4{4,36} | Stericantellated 8-cube Cellirhombated octeract | 752640 | 107520 | ||||||||
| 86 | t0,2,3{4,36} | Runcicantellated 8-cube Prismatorhombated octeract | 193536 | 43008 | ||||||||
| 87 | t0,1,7{4,36} | Heptitruncated 8-cube Exitruncated octeract | 93184 | 14336 | ||||||||
| 88 | t0,1,6{4,36} | Hexitruncated 8-cube Petitruncated octeract | 344064 | 43008 | ||||||||
| 89 | t0,1,5{4,36} | Pentitruncated 8-cube Teritruncated octeract | 609280 | 71680 | ||||||||
| 90 | t0,1,4{4,36} | Steritruncated 8-cube Cellitruncated octeract | 573440 | 71680 | ||||||||
| 91 | t0,1,3{4,36} | Runcitruncated 8-cube Prismatotruncated octeract | 279552 | 43008 | ||||||||
| 92 | t0,1,2{4,36} | Cantitruncated 8-cube Great rhombated octeract | 57344 | 14336 | ||||||||
| 93 | t0,1,2,3{36,4} | Runcicantitruncated 8-orthoplex Great prismated diacosipentacontahexazetton | 147840 | 26880 | ||||||||
| 94 | t0,1,2,4{36,4} | Stericantitruncated 8-orthoplex Celligreatorhombated diacosipentacontahexazetton | 860160 | 107520 | ||||||||
| 95 | t0,1,3,4{36,4} | Steriruncitruncated 8-orthoplex Celliprismatotruncated diacosipentacontahexazetton | 591360 | 107520 | ||||||||
| 96 | t0,2,3,4{36,4} | Steriruncicantellated 8-orthoplex Celliprismatorhombated diacosipentacontahexazetton | 591360 | 107520 | ||||||||
| 97 | t1,2,3,4{36,4} | Biruncicantitruncated 8-orthoplex Great biprismated diacosipentacontahexazetton | 537600 | 107520 | ||||||||
| 98 | t0,1,2,5{36,4} | Penticantitruncated 8-orthoplex Terigreatorhombated diacosipentacontahexazetton | 1827840 | 215040 | ||||||||
| 99 | t0,1,3,5{36,4} | Pentiruncitruncated 8-orthoplex Teriprismatotruncated diacosipentacontahexazetton | 2419200 | 322560 | ||||||||
| 100 | t0,2,3,5{36,4} | Pentiruncicantellated 8-orthoplex Teriprismatorhombated diacosipentacontahexazetton | 2257920 | 322560 | ||||||||
| 101 | t1,2,3,5{36,4} | Bistericantitruncated 8-orthoplex Bicelligreatorhombated diacosipentacontahexazetton | 2096640 | 322560 | ||||||||
| 102 | t0,1,4,5{36,4} | Pentisteritruncated 8-orthoplex Tericellitruncated diacosipentacontahexazetton | 1182720 | 215040 | ||||||||
| 103 | t0,2,4,5{36,4} | Pentistericantellated 8-orthoplex Tericellirhombated diacosipentacontahexazetton | 1935360 | 322560 | ||||||||
| 104 | t1,2,4,5{36,4} | Bisteriruncitruncated 8-orthoplex Bicelliprismatotruncated diacosipentacontahexazetton | 1612800 | 322560 | ||||||||
| 105 | t0,3,4,5{36,4} | Pentisteriruncinated 8-orthoplex Tericelliprismated diacosipentacontahexazetton | 1182720 | 215040 | ||||||||
| 106 | t1,3,4,5{36,4} | Bisteriruncicantellated 8-orthoplex Bicelliprismatorhombated diacosipentacontahexazetton | 1774080 | 322560 | ||||||||
| 107 | t2,3,4,5{4,36} | Triruncicantitruncated 8-cube Great triprismato-octeractidiacosipentacontahexazetton | 967680 | 215040 | ||||||||
| 108 | t0,1,2,6{36,4} | Hexicantitruncated 8-orthoplex Petigreatorhombated diacosipentacontahexazetton | 1505280 | 215040 | ||||||||
| 109 | t0,1,3,6{36,4} | Hexiruncitruncated 8-orthoplex Petiprismatotruncated diacosipentacontahexazetton | 3225600 | 430080 | ||||||||
| 110 | t0,2,3,6{36,4} | Hexiruncicantellated 8-orthoplex Petiprismatorhombated diacosipentacontahexazetton | 2795520 | 430080 | ||||||||
| 111 | t1,2,3,6{36,4} | Bipenticantitruncated 8-orthoplex Biterigreatorhombated diacosipentacontahexazetton | 2580480 | 430080 | ||||||||
| 112 | t0,1,4,6{36,4} | Hexisteritruncated 8-orthoplex Peticellitruncated diacosipentacontahexazetton | 3010560 | 430080 | ||||||||
| 113 | t0,2,4,6{36,4} | Hexistericantellated 8-orthoplex Peticellirhombated diacosipentacontahexazetton | 4515840 | 645120 | ||||||||
| 114 | t1,2,4,6{36,4} | Bipentiruncitruncated 8-orthoplex Biteriprismatotruncated diacosipentacontahexazetton | 3870720 | 645120 | ||||||||
| 115 | t0,3,4,6{36,4} | Hexisteriruncinated 8-orthoplex Peticelliprismated diacosipentacontahexazetton | 2580480 | 430080 | ||||||||
| 116 | t1,3,4,6{4,36} | Bipentiruncicantellated 8-cube Biteriprismatorhombi-octeractidiacosipentacontahexazetton | 3870720 | 645120 | ||||||||
| 117 | t1,3,4,5{4,36} | Bisteriruncicantellated 8-cube Bicelliprismatorhombated octeract | 2150400 | 430080 | ||||||||
| 118 | t0,1,5,6{36,4} | Hexipentitruncated 8-orthoplex Petiteritruncated diacosipentacontahexazetton | 1182720 | 215040 | ||||||||
| 119 | t0,2,5,6{36,4} | Hexipenticantellated 8-orthoplex Petiterirhombated diacosipentacontahexazetton | 2795520 | 430080 | ||||||||
| 120 | t1,2,5,6{4,36} | Bipentisteritruncated 8-cube Bitericellitrunki-octeractidiacosipentacontahexazetton | 2150400 | 430080 | ||||||||
| 121 | t0,3,5,6{36,4} | Hexipentiruncinated 8-orthoplex Petiteriprismated diacosipentacontahexazetton | 2795520 | 430080 | ||||||||
| 122 | t1,2,4,6{4,36} | Bipentiruncitruncated 8-cube Biteriprismatotruncated octeract | 3870720 | 645120 | ||||||||
| 123 | t1,2,4,5{4,36} | Bisteriruncitruncated 8-cube Bicelliprismatotruncated octeract | 1935360 | 430080 | ||||||||
| 124 | t0,4,5,6{36,4} | Hexipentistericated 8-orthoplex Petitericellated diacosipentacontahexazetton | 1182720 | 215040 | ||||||||
| 125 | t1,2,3,6{4,36} | Bipenticantitruncated 8-cube Biterigreatorhombated octeract | 2580480 | 430080 | ||||||||
| 126 | t1,2,3,5{4,36} | Bistericantitruncated 8-cube Bicelligreatorhombated octeract | 2365440 | 430080 | ||||||||
| 127 | t1,2,3,4{4,36} | Biruncicantitruncated 8-cube Great biprismated octeract | 860160 | 215040 | ||||||||
| 128 | t0,1,2,7{36,4} | Hepticantitruncated 8-orthoplex Exigreatorhombated diacosipentacontahexazetton | 516096 | 86016 | ||||||||
| 129 | t0,1,3,7{36,4} | Heptiruncitruncated 8-orthoplex Exiprismatotruncated diacosipentacontahexazetton | 1612800 | 215040 | ||||||||
| 130 | t0,2,3,7{36,4} | Heptiruncicantellated 8-orthoplex Exiprismatorhombated diacosipentacontahexazetton | 1290240 | 215040 | ||||||||
| 131 | t0,4,5,6{4,36} | Hexipentistericated 8-cube Petitericellated octeract | 1182720 | 215040 | ||||||||
| 132 | t0,1,4,7{36,4} | Heptisteritruncated 8-orthoplex Exicellitruncated diacosipentacontahexazetton | 2293760 | 286720 | ||||||||
| 133 | t0,2,4,7{36,4} | Heptistericantellated 8-orthoplex Exicellirhombated diacosipentacontahexazetton | 3225600 | 430080 | ||||||||
| 134 | t0,3,5,6{4,36} | Hexipentiruncinated 8-cube Petiteriprismated octeract | 2795520 | 430080 | ||||||||
| 135 | t0,3,4,7{4,36} | Heptisteriruncinated 8-cube Exicelliprismato-octeractidiacosipentacontahexazetton | 1720320 | 286720 | ||||||||
| 136 | t0,3,4,6{4,36} | Hexisteriruncinated 8-cube Peticelliprismated octeract | 2580480 | 430080 | ||||||||
| 137 | t0,3,4,5{4,36} | Pentisteriruncinated 8-cube Tericelliprismated octeract | 1433600 | 286720 | ||||||||
| 138 | t0,1,5,7{36,4} | Heptipentitruncated 8-orthoplex Exiteritruncated diacosipentacontahexazetton | 1612800 | 215040 | ||||||||
| 139 | t0,2,5,7{4,36} | Heptipenticantellated 8-cube Exiterirhombi-octeractidiacosipentacontahexazetton | 3440640 | 430080 | ||||||||
| 140 | t0,2,5,6{4,36} | Hexipenticantellated 8-cube Petiterirhombated octeract | 2795520 | 430080 | ||||||||
| 141 | t0,2,4,7{4,36} | Heptistericantellated 8-cube Exicellirhombated octeract | 3225600 | 430080 | ||||||||
| 142 | t0,2,4,6{4,36} | Hexistericantellated 8-cube Peticellirhombated octeract | 4515840 | 645120 | ||||||||
| 143 | t0,2,4,5{4,36} | Pentistericantellated 8-cube Tericellirhombated octeract | 2365440 | 430080 | ||||||||
| 144 | t0,2,3,7{4,36} | Heptiruncicantellated 8-cube Exiprismatorhombated octeract | 1290240 | 215040 | ||||||||
| 145 | t0,2,3,6{4,36} | Hexiruncicantellated 8-cube Petiprismatorhombated octeract | 2795520 | 430080 | ||||||||
| 146 | t0,2,3,5{4,36} | Pentiruncicantellated 8-cube Teriprismatorhombated octeract | 2580480 | 430080 | ||||||||
| 147 | t0,2,3,4{4,36} | Steriruncicantellated 8-cube Celliprismatorhombated octeract | 967680 | 215040 | ||||||||
| 148 | t0,1,6,7{4,36} | Heptihexitruncated 8-cube Exipetitrunki-octeractidiacosipentacontahexazetton | 516096 | 86016 | ||||||||
| 149 | t0,1,5,7{4,36} | Heptipentitruncated 8-cube Exiteritruncated octeract | 1612800 | 215040 | ||||||||
| 150 | t0,1,5,6{4,36} | Hexipentitruncated 8-cube Petiteritruncated octeract | 1182720 | 215040 | ||||||||
| 151 | t0,1,4,7{4,36} | Heptisteritruncated 8-cube Exicellitruncated octeract | 2293760 | 286720 | ||||||||
| 152 | t0,1,4,6{4,36} | Hexisteritruncated 8-cube Peticellitruncated octeract | 3010560 | 430080 | ||||||||
| 153 | t0,1,4,5{4,36} | Pentisteritruncated 8-cube Tericellitruncated octeract | 1433600 | 286720 | ||||||||
| 154 | t0,1,3,7{4,36} | Heptiruncitruncated 8-cube Exiprismatotruncated octeract | 1612800 | 215040 | ||||||||
| 155 | t0,1,3,6{4,36} | Hexiruncitruncated 8-cube Petiprismatotruncated octeract | 3225600 | 430080 | ||||||||
| 156 | t0,1,3,5{4,36} | Pentiruncitruncated 8-cube Teriprismatotruncated octeract | 2795520 | 430080 | ||||||||
| 157 | t0,1,3,4{4,36} | Steriruncitruncated 8-cube Celliprismatotruncated octeract | 967680 | 215040 | ||||||||
| 158 | t0,1,2,7{4,36} | Hepticantitruncated 8-cube Exigreatorhombated octeract | 516096 | 86016 | ||||||||
| 159 | t0,1,2,6{4,36} | Hexicantitruncated 8-cube Petigreatorhombated octeract | 1505280 | 215040 | ||||||||
| 160 | t0,1,2,5{4,36} | Penticantitruncated 8-cube Terigreatorhombated octeract | 2007040 | 286720 | ||||||||
| 161 | t0,1,2,4{4,36} | Stericantitruncated 8-cube Celligreatorhombated octeract | 1290240 | 215040 | ||||||||
| 162 | t0,1,2,3{4,36} | Runcicantitruncated 8-cube Great prismated octeract | 344064 | 86016 | ||||||||
| 163 | t0,1,2,3,4{36,4} | Steriruncicantitruncated 8-orthoplex Great cellated diacosipentacontahexazetton | 1075200 | 215040 | ||||||||
| 164 | t0,1,2,3,5{36,4} | Pentiruncicantitruncated 8-orthoplex Terigreatoprismated diacosipentacontahexazetton | 4193280 | 645120 | ||||||||
| 165 | t0,1,2,4,5{36,4} | Pentistericantitruncated 8-orthoplex Tericelligreatorhombated diacosipentacontahexazetton | 3225600 | 645120 | ||||||||
| 166 | t0,1,3,4,5{36,4} | Pentisteriruncitruncated 8-orthoplex Tericelliprismatotruncated diacosipentacontahexazetton | 3225600 | 645120 | ||||||||
| 167 | t0,2,3,4,5{36,4} | Pentisteriruncicantellated 8-orthoplex Tericelliprismatorhombated diacosipentacontahexazetton | 3225600 | 645120 | ||||||||
| 168 | t1,2,3,4,5{36,4} | Bisteriruncicantitruncated 8-orthoplex Great bicellated diacosipentacontahexazetton | 2903040 | 645120 | ||||||||
| 169 | t0,1,2,3,6{36,4} | Hexiruncicantitruncated 8-orthoplex Petigreatoprismated diacosipentacontahexazetton | 5160960 | 860160 | ||||||||
| 170 | t0,1,2,4,6{36,4} | Hexistericantitruncated 8-orthoplex Peticelligreatorhombated diacosipentacontahexazetton | 7741440 | 1290240 | ||||||||
| 171 | t0,1,3,4,6{36,4} | Hexisteriruncitruncated 8-orthoplex Peticelliprismatotruncated diacosipentacontahexazetton | 7096320 | 1290240 | ||||||||
| 172 | t0,2,3,4,6{36,4} | Hexisteriruncicantellated 8-orthoplex Peticelliprismatorhombated diacosipentacontahexazetton | 7096320 | 1290240 | ||||||||
| 173 | t1,2,3,4,6{36,4} | Bipentiruncicantitruncated 8-orthoplex Biterigreatoprismated diacosipentacontahexazetton | 6451200 | 1290240 | ||||||||
| 174 | t0,1,2,5,6{36,4} | Hexipenticantitruncated 8-orthoplex Petiterigreatorhombated diacosipentacontahexazetton | 4300800 | 860160 | ||||||||
| 175 | t0,1,3,5,6{36,4} | Hexipentiruncitruncated 8-orthoplex Petiteriprismatotruncated diacosipentacontahexazetton | 7096320 | 1290240 | ||||||||
| 176 | t0,2,3,5,6{36,4} | Hexipentiruncicantellated 8-orthoplex Petiteriprismatorhombated diacosipentacontahexazetton | 6451200 | 1290240 | ||||||||
| 177 | t1,2,3,5,6{36,4} | Bipentistericantitruncated 8-orthoplex Bitericelligreatorhombated diacosipentacontahexazetton | 5806080 | 1290240 | ||||||||
| 178 | t0,1,4,5,6{36,4} | Hexipentisteritruncated 8-orthoplex Petitericellitruncated diacosipentacontahexazetton | 4300800 | 860160 | ||||||||
| 179 | t0,2,4,5,6{36,4} | Hexipentistericantellated 8-orthoplex Petitericellirhombated diacosipentacontahexazetton | 7096320 | 1290240 | ||||||||
| 180 | t1,2,3,5,6{4,36} | Bipentistericantitruncated 8-cube Bitericelligreatorhombated octeract | 5806080 | 1290240 | ||||||||
| 181 | t0,3,4,5,6{36,4} | Hexipentisteriruncinated 8-orthoplex Petitericelliprismated diacosipentacontahexazetton | 4300800 | 860160 | ||||||||
| 182 | t1,2,3,4,6{4,36} | Bipentiruncicantitruncated 8-cube Biterigreatoprismated octeract | 6451200 | 1290240 | ||||||||
| 183 | t1,2,3,4,5{4,36} | Bisteriruncicantitruncated 8-cube Great bicellated octeract | 3440640 | 860160 | ||||||||
| 184 | t0,1,2,3,7{36,4} | Heptiruncicantitruncated 8-orthoplex Exigreatoprismated diacosipentacontahexazetton | 2365440 | 430080 | ||||||||
| 185 | t0,1,2,4,7{36,4} | Heptistericantitruncated 8-orthoplex Exicelligreatorhombated diacosipentacontahexazetton | 5591040 | 860160 | ||||||||
| 186 | t0,1,3,4,7{36,4} | Heptisteriruncitruncated 8-orthoplex Exicelliprismatotruncated diacosipentacontahexazetton | 4730880 | 860160 | ||||||||
| 187 | t0,2,3,4,7{36,4} | Heptisteriruncicantellated 8-orthoplex Exicelliprismatorhombated diacosipentacontahexazetton | 4730880 | 860160 | ||||||||
| 188 | t0,3,4,5,6{4,36} | Hexipentisteriruncinated 8-cube Petitericelliprismated octeract | 4300800 | 860160 | ||||||||
| 189 | t0,1,2,5,7{36,4} | Heptipenticantitruncated 8-orthoplex Exiterigreatorhombated diacosipentacontahexazetton | 5591040 | 860160 | ||||||||
| 190 | t0,1,3,5,7{36,4} | Heptipentiruncitruncated 8-orthoplex Exiteriprismatotruncated diacosipentacontahexazetton | 8386560 | 1290240 | ||||||||
| 191 | t0,2,3,5,7{36,4} | Heptipentiruncicantellated 8-orthoplex Exiteriprismatorhombated diacosipentacontahexazetton | 7741440 | 1290240 | ||||||||
| 192 | t0,2,4,5,6{4,36} | Hexipentistericantellated 8-cube Petitericellirhombated octeract | 7096320 | 1290240 | ||||||||
| 193 | t0,1,4,5,7{36,4} | Heptipentisteritruncated 8-orthoplex Exitericellitruncated diacosipentacontahexazetton | 4730880 | 860160 | ||||||||
| 194 | t0,2,3,5,7{4,36} | Heptipentiruncicantellated 8-cube Exiteriprismatorhombated octeract | 7741440 | 1290240 | ||||||||
| 195 | t0,2,3,5,6{4,36} | Hexipentiruncicantellated 8-cube Petiteriprismatorhombated octeract | 6451200 | 1290240 | ||||||||
| 196 | t0,2,3,4,7{4,36} | Heptisteriruncicantellated 8-cube Exicelliprismatorhombated octeract | 4730880 | 860160 | ||||||||
| 197 | t0,2,3,4,6{4,36} | Hexisteriruncicantellated 8-cube Peticelliprismatorhombated octeract | 7096320 | 1290240 | ||||||||
| 198 | t0,2,3,4,5{4,36} | Pentisteriruncicantellated 8-cube Tericelliprismatorhombated octeract | 3870720 | 860160 | ||||||||
| 199 | t0,1,2,6,7{36,4} | Heptihexicantitruncated 8-orthoplex Exipetigreatorhombated diacosipentacontahexazetton | 2365440 | 430080 | ||||||||
| 200 | t0,1,3,6,7{36,4} | Heptihexiruncitruncated 8-orthoplex Exipetiprismatotruncated diacosipentacontahexazetton | 5591040 | 860160 | ||||||||
| 201 | t0,1,4,5,7{4,36} | Heptipentisteritruncated 8-cube Exitericellitruncated octeract | 4730880 | 860160 | ||||||||
| 202 | t0,1,4,5,6{4,36} | Hexipentisteritruncated 8-cube Petitericellitruncated octeract | 4300800 | 860160 | ||||||||
| 203 | t0,1,3,6,7{4,36} | Heptihexiruncitruncated 8-cube Exipetiprismatotruncated octeract | 5591040 | 860160 | ||||||||
| 204 | t0,1,3,5,7{4,36} | Heptipentiruncitruncated 8-cube Exiteriprismatotruncated octeract | 8386560 | 1290240 | ||||||||
| 205 | t0,1,3,5,6{4,36} | Hexipentiruncitruncated 8-cube Petiteriprismatotruncated octeract | 7096320 | 1290240 | ||||||||
| 206 | t0,1,3,4,7{4,36} | Heptisteriruncitruncated 8-cube Exicelliprismatotruncated octeract | 4730880 | 860160 | ||||||||
| 207 | t0,1,3,4,6{4,36} | Hexisteriruncitruncated 8-cube Peticelliprismatotruncated octeract | 7096320 | 1290240 | ||||||||
| 208 | t0,1,3,4,5{4,36} | Pentisteriruncitruncated 8-cube Tericelliprismatotruncated octeract | 3870720 | 860160 | ||||||||
| 209 | t0,1,2,6,7{4,36} | Heptihexicantitruncated 8-cube Exipetigreatorhombated octeract | 2365440 | 430080 | ||||||||
| 210 | t0,1,2,5,7{4,36} | Heptipenticantitruncated 8-cube Exiterigreatorhombated octeract | 5591040 | 860160 | ||||||||
| 211 | t0,1,2,5,6{4,36} | Hexipenticantitruncated 8-cube Petiterigreatorhombated octeract | 4300800 | 860160 | ||||||||
| 212 | t0,1,2,4,7{4,36} | Heptistericantitruncated 8-cube Exicelligreatorhombated octeract | 5591040 | 860160 | ||||||||
| 213 | t0,1,2,4,6{4,36} | Hexistericantitruncated 8-cube Peticelligreatorhombated octeract | 7741440 | 1290240 | ||||||||
| 214 | t0,1,2,4,5{4,36} | Pentistericantitruncated 8-cube Tericelligreatorhombated octeract | 3870720 | 860160 | ||||||||
| 215 | t0,1,2,3,7{4,36} | Heptiruncicantitruncated 8-cube Exigreatoprismated octeract | 2365440 | 430080 | ||||||||
| 216 | t0,1,2,3,6{4,36} | Hexiruncicantitruncated 8-cube Petigreatoprismated octeract | 5160960 | 860160 | ||||||||
| 217 | t0,1,2,3,5{4,36} | Pentiruncicantitruncated 8-cube Terigreatoprismated octeract | 4730880 | 860160 | ||||||||
| 218 | t0,1,2,3,4{4,36} | Steriruncicantitruncated 8-cube Great cellated octeract | 1720320 | 430080 | ||||||||
| 219 | t0,1,2,3,4,5{36,4} | Pentisteriruncicantitruncated 8-orthoplex Great terated diacosipentacontahexazetton | 5806080 | 1290240 | ||||||||
| 220 | t0,1,2,3,4,6{36,4} | Hexisteriruncicantitruncated 8-orthoplex Petigreatocellated diacosipentacontahexazetton | 12902400 | 2580480 | ||||||||
| 221 | t0,1,2,3,5,6{36,4} | Hexipentiruncicantitruncated 8-orthoplex Petiterigreatoprismated diacosipentacontahexazetton | 11612160 | 2580480 | ||||||||
| 222 | t0,1,2,4,5,6{36,4} | Hexipentistericantitruncated 8-orthoplex Petitericelligreatorhombated diacosipentacontahexazetton | 11612160 | 2580480 | ||||||||
| 223 | t0,1,3,4,5,6{36,4} | Hexipentisteriruncitruncated 8-orthoplex Petitericelliprismatotruncated diacosipentacontahexazetton | 11612160 | 2580480 | ||||||||
| 224 | t0,2,3,4,5,6{36,4} | Hexipentisteriruncicantellated 8-orthoplex Petitericelliprismatorhombated diacosipentacontahexazetton | 11612160 | 2580480 | ||||||||
| 225 | t1,2,3,4,5,6{4,36} | Bipentisteriruncicantitruncated 8-cube Great biteri-octeractidiacosipentacontahexazetton | 10321920 | 2580480 | ||||||||
| 226 | t0,1,2,3,4,7{36,4} | Heptisteriruncicantitruncated 8-orthoplex Exigreatocellated diacosipentacontahexazetton | 8601600 | 1720320 | ||||||||
| 227 | t0,1,2,3,5,7{36,4} | Heptipentiruncicantitruncated 8-orthoplex Exiterigreatoprismated diacosipentacontahexazetton | 14192640 | 2580480 | ||||||||
| 228 | t0,1,2,4,5,7{36,4} | Heptipentistericantitruncated 8-orthoplex Exitericelligreatorhombated diacosipentacontahexazetton | 12902400 | 2580480 | ||||||||
| 229 | t0,1,3,4,5,7{36,4} | Heptipentisteriruncitruncated 8-orthoplex Exitericelliprismatotruncated diacosipentacontahexazetton | 12902400 | 2580480 | ||||||||
| 230 | t0,2,3,4,5,7{4,36} | Heptipentisteriruncicantellated 8-cube Exitericelliprismatorhombi-octeractidiacosipentacontahexazetton | 12902400 | 2580480 | ||||||||
| 231 | t0,2,3,4,5,6{4,36} | Hexipentisteriruncicantellated 8-cube Petitericelliprismatorhombated octeract | 11612160 | 2580480 | ||||||||
| 232 | t0,1,2,3,6,7{36,4} | Heptihexiruncicantitruncated 8-orthoplex Exipetigreatoprismated diacosipentacontahexazetton | 8601600 | 1720320 | ||||||||
| 233 | t0,1,2,4,6,7{36,4} | Heptihexistericantitruncated 8-orthoplex Exipeticelligreatorhombated diacosipentacontahexazetton | 14192640 | 2580480 | ||||||||
| 234 | t0,1,3,4,6,7{4,36} | Heptihexisteriruncitruncated 8-cube Exipeticelliprismatotrunki-octeractidiacosipentacontahexazetton | 12902400 | 2580480 | ||||||||
| 235 | t0,1,3,4,5,7{4,36} | Heptipentisteriruncitruncated 8-cube Exitericelliprismatotruncated octeract | 12902400 | 2580480 | ||||||||
| 236 | t0,1,3,4,5,6{4,36} | Hexipentisteriruncitruncated 8-cube Petitericelliprismatotruncated octeract | 11612160 | 2580480 | ||||||||
| 237 | t0,1,2,5,6,7{4,36} | Heptihexipenticantitruncated 8-cube Exipetiterigreatorhombi-octeractidiacosipentacontahexazetton | 8601600 | 1720320 | ||||||||
| 238 | t0,1,2,4,6,7{4,36} | Heptihexistericantitruncated 8-cube Exipeticelligreatorhombated octeract | 14192640 | 2580480 | ||||||||
| 239 | t0,1,2,4,5,7{4,36} | Heptipentistericantitruncated 8-cube Exitericelligreatorhombated octeract | 12902400 | 2580480 | ||||||||
| 240 | t0,1,2,4,5,6{4,36} | Hexipentistericantitruncated 8-cube Petitericelligreatorhombated octeract | 11612160 | 2580480 | ||||||||
| 241 | t0,1,2,3,6,7{4,36} | Heptihexiruncicantitruncated 8-cube Exipetigreatoprismated octeract | 8601600 | 1720320 | ||||||||
| 242 | t0,1,2,3,5,7{4,36} | Heptipentiruncicantitruncated 8-cube Exiterigreatoprismated octeract | 14192640 | 2580480 | ||||||||
| 243 | t0,1,2,3,5,6{4,36} | Hexipentiruncicantitruncated 8-cube Petiterigreatoprismated octeract | 11612160 | 2580480 | ||||||||
| 244 | t0,1,2,3,4,7{4,36} | Heptisteriruncicantitruncated 8-cube Exigreatocellated octeract | 8601600 | 1720320 | ||||||||
| 245 | t0,1,2,3,4,6{4,36} | Hexisteriruncicantitruncated 8-cube Petigreatocellated octeract | 12902400 | 2580480 | ||||||||
| 246 | t0,1,2,3,4,5{4,36} | Pentisteriruncicantitruncated 8-cube Great terated octeract | 6881280 | 1720320 | ||||||||
| 247 | t0,1,2,3,4,5,6{36,4} | Hexipentisteriruncicantitruncated 8-orthoplex Great petated diacosipentacontahexazetton | 20643840 | 5160960 | ||||||||
| 248 | t0,1,2,3,4,5,7{36,4} | Heptipentisteriruncicantitruncated 8-orthoplex Exigreatoterated diacosipentacontahexazetton | 23224320 | 5160960 | ||||||||
| 249 | t0,1,2,3,4,6,7{36,4} | Heptihexisteriruncicantitruncated 8-orthoplex Exipetigreatocellated diacosipentacontahexazetton | 23224320 | 5160960 | ||||||||
| 250 | t0,1,2,3,5,6,7{36,4} | Heptihexipentiruncicantitruncated 8-orthoplex Exipetiterigreatoprismated diacosipentacontahexazetton | 23224320 | 5160960 | ||||||||
| 251 | t0,1,2,3,5,6,7{4,36} | Heptihexipentiruncicantitruncated 8-cube Exipetiterigreatoprismated octeract | 23224320 | 5160960 | ||||||||
| 252 | t0,1,2,3,4,6,7{4,36} | Heptihexisteriruncicantitruncated 8-cube Exipetigreatocellated octeract | 23224320 | 5160960 | ||||||||
| 253 | t0,1,2,3,4,5,7{4,36} | Heptipentisteriruncicantitruncated 8-cube Exigreatoterated octeract | 23224320 | 5160960 | ||||||||
| 254 | t0,1,2,3,4,5,6{4,36} | Hexipentisteriruncicantitruncated 8-cube Great petated octeract | 20643840 | 5160960 | ||||||||
| 255 | t0,1,2,3,4,5,6,7{4,36} | Omnitruncated 8-cube Great exi-octeractidiacosipentacontahexazetton | 41287680 | 10321920 | ||||||||
The D8 family
The D8 family has symmetry of order 5,160,960 (8 factorial x 27).
This family has 191 Wythoffian uniform polytopes, from 3x64-1 permutations of the D8 Coxeter-Dynkin diagram with one or more rings. 127 (2x64-1) are repeated from the B8 family and 64 are unique to this family, all listed below.
See list of D8 polytopes for Coxeter plane graphs of these polytopes.
| D8 uniform polytopes | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # | Coxeter-Dynkin diagram | Name | Base point (Alternately signed) |
Element counts | Circumrad | |||||||||
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | |||||||
| 1 | = | 8-demicube h{4,3,3,3,3,3,3} | (1,1,1,1,1,1,1,1) | 144 | 1136 | 4032 | 8288 | 10752 | 7168 | 1792 | 128 | 1.0000000 | ||
| 2 | = | cantic 8-cube h2{4,3,3,3,3,3,3} | (1,1,3,3,3,3,3,3) | 23296 | 3584 | 2.6457512 | ||||||||
| 3 | = | runcic 8-cube h3{4,3,3,3,3,3,3} | (1,1,1,3,3,3,3,3) | 64512 | 7168 | 2.4494896 | ||||||||
| 4 | = | steric 8-cube h4{4,3,3,3,3,3,3} | (1,1,1,1,3,3,3,3) | 98560 | 8960 | 2.2360678 | ||||||||
| 5 | = | pentic 8-cube h5{4,3,3,3,3,3,3} | (1,1,1,1,1,3,3,3) | 89600 | 7168 | 1.9999999 | ||||||||
| 6 | = | hexic 8-cube h6{4,3,3,3,3,3,3} | (1,1,1,1,1,1,3,3) | 48384 | 3584 | 1.7320508 | ||||||||
| 7 | = | heptic 8-cube h7{4,3,3,3,3,3,3} | (1,1,1,1,1,1,1,3) | 14336 | 1024 | 1.4142135 | ||||||||
| 8 | = | runcicantic 8-cube h2,3{4,3,3,3,3,3,3} | (1,1,3,5,5,5,5,5) | 86016 | 21504 | 4.1231055 | ||||||||
| 9 | = | stericantic 8-cube h2,4{4,3,3,3,3,3,3} | (1,1,3,3,5,5,5,5) | 349440 | 53760 | 3.8729835 | ||||||||
| 10 | = | steriruncic 8-cube h3,4{4,3,3,3,3,3,3} | (1,1,1,3,5,5,5,5) | 179200 | 35840 | 3.7416575 | ||||||||
| 11 | = | penticantic 8-cube h2,5{4,3,3,3,3,3,3} | (1,1,3,3,3,5,5,5) | 573440 | 71680 | 3.6055512 | ||||||||
| 12 | = | pentiruncic 8-cube h3,5{4,3,3,3,3,3,3} | (1,1,1,3,3,5,5,5) | 537600 | 71680 | 3.4641016 | ||||||||
| 13 | = | pentisteric 8-cube h4,5{4,3,3,3,3,3,3} | (1,1,1,1,3,5,5,5) | 232960 | 35840 | 3.3166249 | ||||||||
| 14 | = | hexicantic 8-cube h2,6{4,3,3,3,3,3,3} | (1,1,3,3,3,3,5,5) | 456960 | 53760 | 3.3166249 | ||||||||
| 15 | = | hexicruncic 8-cube h3,6{4,3,3,3,3,3,3} | (1,1,1,3,3,3,5,5) | 645120 | 71680 | 3.1622777 | ||||||||
| 16 | = | hexisteric 8-cube h4,6{4,3,3,3,3,3,3} | (1,1,1,1,3,3,5,5) | 483840 | 53760 | 3 | ||||||||
| 17 | = | hexipentic 8-cube h5,6{4,3,3,3,3,3,3} | (1,1,1,1,1,3,5,5) | 182784 | 21504 | 2.8284271 | ||||||||
| 18 | = | hepticantic 8-cube h2,7{4,3,3,3,3,3,3} | (1,1,3,3,3,3,3,5) | 172032 | 21504 | 3 | ||||||||
| 19 | = | heptiruncic 8-cube h3,7{4,3,3,3,3,3,3} | (1,1,1,3,3,3,3,5) | 340480 | 35840 | 2.8284271 | ||||||||
| 20 | = | heptsteric 8-cube h4,7{4,3,3,3,3,3,3} | (1,1,1,1,3,3,3,5) | 376320 | 35840 | 2.6457512 | ||||||||
| 21 | = | heptipentic 8-cube h5,7{4,3,3,3,3,3,3} | (1,1,1,1,1,3,3,5) | 236544 | 21504 | 2.4494898 | ||||||||
| 22 | = | heptihexic 8-cube h6,7{4,3,3,3,3,3,3} | (1,1,1,1,1,1,3,5) | 78848 | 7168 | 2.236068 | ||||||||
| 23 | = | steriruncicantic 8-cube h2,3,4{4,36} | (1,1,3,5,7,7,7,7) | 430080 | 107520 | 5.3851647 | ||||||||
| 24 | = | pentiruncicantic 8-cube h2,3,5{4,36} | (1,1,3,5,5,7,7,7) | 1182720 | 215040 | 5.0990195 | ||||||||
| 25 | = | pentistericantic 8-cube h2,4,5{4,36} | (1,1,3,3,5,7,7,7) | 1075200 | 215040 | 4.8989797 | ||||||||
| 26 | = | pentisterirunic 8-cube h3,4,5{4,36} | (1,1,1,3,5,7,7,7) | 716800 | 143360 | 4.7958317 | ||||||||
| 27 | = | hexiruncicantic 8-cube h2,3,6{4,36} | (1,1,3,5,5,5,7,7) | 1290240 | 215040 | 4.7958317 | ||||||||
| 28 | = | hexistericantic 8-cube h2,4,6{4,36} | (1,1,3,3,5,5,7,7) | 2096640 | 322560 | 4.5825758 | ||||||||
| 29 | = | hexisterirunic 8-cube h3,4,6{4,36} | (1,1,1,3,5,5,7,7) | 1290240 | 215040 | 4.472136 | ||||||||
| 30 | = | hexipenticantic 8-cube h2,5,6{4,36} | (1,1,3,3,3,5,7,7) | 1290240 | 215040 | 4.3588991 | ||||||||
| 31 | = | hexipentirunic 8-cube h3,5,6{4,36} | (1,1,1,3,3,5,7,7) | 1397760 | 215040 | 4.2426405 | ||||||||
| 32 | = | hexipentisteric 8-cube h4,5,6{4,36} | (1,1,1,1,3,5,7,7) | 698880 | 107520 | 4.1231055 | ||||||||
| 33 | = | heptiruncicantic 8-cube h2,3,7{4,36} | (1,1,3,5,5,5,5,7) | 591360 | 107520 | 4.472136 | ||||||||
| 34 | = | heptistericantic 8-cube h2,4,7{4,36} | (1,1,3,3,5,5,5,7) | 1505280 | 215040 | 4.2426405 | ||||||||
| 35 | = | heptisterruncic 8-cube h3,4,7{4,36} | (1,1,1,3,5,5,5,7) | 860160 | 143360 | 4.1231055 | ||||||||
| 36 | = | heptipenticantic 8-cube h2,5,7{4,36} | (1,1,3,3,3,5,5,7) | 1612800 | 215040 | 4 | ||||||||
| 37 | = | heptipentiruncic 8-cube h3,5,7{4,36} | (1,1,1,3,3,5,5,7) | 1612800 | 215040 | 3.8729835 | ||||||||
| 38 | = | heptipentisteric 8-cube h4,5,7{4,36} | (1,1,1,1,3,5,5,7) | 752640 | 107520 | 3.7416575 | ||||||||
| 39 | = | heptihexicantic 8-cube h2,6,7{4,36} | (1,1,3,3,3,3,5,7) | 752640 | 107520 | 3.7416575 | ||||||||
| 40 | = | heptihexiruncic 8-cube h3,6,7{4,36} | (1,1,1,3,3,3,5,7) | 1146880 | 143360 | 3.6055512 | ||||||||
| 41 | = | heptihexisteric 8-cube h4,6,7{4,36} | (1,1,1,1,3,3,5,7) | 913920 | 107520 | 3.4641016 | ||||||||
| 42 | = | heptihexipentic 8-cube h5,6,7{4,36} | (1,1,1,1,1,3,5,7) | 365568 | 43008 | 3.3166249 | ||||||||
| 43 | = | pentisteriruncicantic 8-cube h2,3,4,5{4,36} | (1,1,3,5,7,9,9,9) | 1720320 | 430080 | 6.4031243 | ||||||||
| 44 | = | hexisteriruncicantic 8-cube h2,3,4,6{4,36} | (1,1,3,5,7,7,9,9) | 3225600 | 645120 | 6.0827627 | ||||||||
| 45 | = | hexipentiruncicantic 8-cube h2,3,5,6{4,36} | (1,1,3,5,5,7,9,9) | 2903040 | 645120 | 5.8309517 | ||||||||
| 46 | = | hexipentistericantic 8-cube h2,4,5,6{4,36} | (1,1,3,3,5,7,9,9) | 3225600 | 645120 | 5.6568542 | ||||||||
| 47 | = | hexipentisteriruncic 8-cube h3,4,5,6{4,36} | (1,1,1,3,5,7,9,9) | 2150400 | 430080 | 5.5677648 | ||||||||
| 48 | = | heptsteriruncicantic 8-cube h2,3,4,7{4,36} | (1,1,3,5,7,7,7,9) | 2150400 | 430080 | 5.7445626 | ||||||||
| 49 | = | heptipentiruncicantic 8-cube h2,3,5,7{4,36} | (1,1,3,5,5,7,7,9) | 3548160 | 645120 | 5.4772258 | ||||||||
| 50 | = | heptipentistericantic 8-cube h2,4,5,7{4,36} | (1,1,3,3,5,7,7,9) | 3548160 | 645120 | 5.291503 | ||||||||
| 51 | = | heptipentisteriruncic 8-cube h3,4,5,7{4,36} | (1,1,1,3,5,7,7,9) | 2365440 | 430080 | 5.1961527 | ||||||||
| 52 | = | heptihexiruncicantic 8-cube h2,3,6,7{4,36} | (1,1,3,5,5,5,7,9) | 2150400 | 430080 | 5.1961527 | ||||||||
| 53 | = | heptihexistericantic 8-cube h2,4,6,7{4,36} | (1,1,3,3,5,5,7,9) | 3870720 | 645120 | 5 | ||||||||
| 54 | = | heptihexisteriruncic 8-cube h3,4,6,7{4,36} | (1,1,1,3,5,5,7,9) | 2365440 | 430080 | 4.8989797 | ||||||||
| 55 | = | heptihexipenticantic 8-cube h2,5,6,7{4,36} | (1,1,3,3,3,5,7,9) | 2580480 | 430080 | 4.7958317 | ||||||||
| 56 | = | heptihexipentiruncic 8-cube h3,5,6,7{4,36} | (1,1,1,3,3,5,7,9) | 2795520 | 430080 | 4.6904159 | ||||||||
| 57 | = | heptihexipentisteric 8-cube h4,5,6,7{4,36} | (1,1,1,1,3,5,7,9) | 1397760 | 215040 | 4.5825758 | ||||||||
| 58 | = | hexipentisteriruncicantic 8-cube h2,3,4,5,6{4,36} | (1,1,3,5,7,9,11,11) | 5160960 | 1290240 | 7.1414285 | ||||||||
| 59 | = | heptipentisteriruncicantic 8-cube h2,3,4,5,7{4,36} | (1,1,3,5,7,9,9,11) | 5806080 | 1290240 | 6.78233 | ||||||||
| 60 | = | heptihexisteriruncicantic 8-cube h2,3,4,6,7{4,36} | (1,1,3,5,7,7,9,11) | 5806080 | 1290240 | 6.480741 | ||||||||
| 61 | = | heptihexipentiruncicantic 8-cube h2,3,5,6,7{4,36} | (1,1,3,5,5,7,9,11) | 5806080 | 1290240 | 6.244998 | ||||||||
| 62 | = | heptihexipentistericantic 8-cube h2,4,5,6,7{4,36} | (1,1,3,3,5,7,9,11) | 6451200 | 1290240 | 6.0827627 | ||||||||
| 63 | = | heptihexipentisteriruncic 8-cube h3,4,5,6,7{4,36} | (1,1,1,3,5,7,9,11) | 4300800 | 860160 | 6.0000000 | ||||||||
| 64 | = | heptihexipentisteriruncicantic 8-cube h2,3,4,5,6,7{4,36} | (1,1,3,5,7,9,11,13) | 2580480 | 10321920 | 7.5498347 | ||||||||
The E8 family
The E8 family has symmetry order 696,729,600.
There are 255 forms based on all permutations of the Coxeter-Dynkin diagrams with one or more rings. Eight forms are shown below, 4 single-ringed, 3 truncations (2 rings), and the final omnitruncation are given below. Bowers-style acronym names are given for cross-referencing.
See also list of E8 polytopes for Coxeter plane graphs of this family.
| E8 uniform polytopes | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # | Coxeter-Dynkin diagram |
Names | Element counts | |||||||||||
| 7-faces | 6-faces | 5-faces | 4-faces | Cells | Faces | Edges | Vertices | |||||||
| 1 | 421 (fy) | 19440 | 207360 | 483840 | 483840 | 241920 | 60480 | 6720 | 240 | |||||
| 2 | Truncated 421 (tiffy) | 188160 | 13440 | |||||||||||
| 3 | Rectified 421 (riffy) | 19680 | 375840 | 1935360 | 3386880 | 2661120 | 1028160 | 181440 | 6720 | |||||
| 4 | Birectified 421 (borfy) | 19680 | 382560 | 2600640 | 7741440 | 9918720 | 5806080 | 1451520 | 60480 | |||||
| 5 | Trirectified 421 (torfy) | 19680 | 382560 | 2661120 | 9313920 | 16934400 | 14515200 | 4838400 | 241920 | |||||
| 6 | Rectified 142 (buffy) | 19680 | 382560 | 2661120 | 9072000 | 16934400 | 16934400 | 7257600 | 483840 | |||||
| 7 | Rectified 241 (robay) | 19680 | 313440 | 1693440 | 4717440 | 7257600 | 5322240 | 1451520 | 69120 | |||||
| 8 | 241 (bay) | 17520 | 144960 | 544320 | 1209600 | 1209600 | 483840 | 69120 | 2160 | |||||
| 9 | Truncated 241 | 138240 | ||||||||||||
| 10 | 142 (bif) | 2400 | 106080 | 725760 | 2298240 | 3628800 | 2419200 | 483840 | 17280 | |||||
| 11 | Truncated 142 | 967680 | ||||||||||||
| 12 | Omnitruncated 421 | 696729600 | ||||||||||||
Regular and uniform honeycombs
There are five fundamental affine Coxeter groups that generate regular and uniform tessellations in 7-space:
| # | Coxeter group | Coxeter diagram | Forms | |
|---|---|---|---|---|
| 1 | [3[8]] | 29 | ||
| 2 | [4,35,4] | 135 | ||
| 3 | [4,34,31,1] | 191 (64 new) | ||
| 4 | [31,1,33,31,1] | 77 (10 new) | ||
| 5 | [33,3,1] | 143 | ||
Regular and uniform tessellations include:
- 29 uniquely ringed forms, including:
- 7-simplex honeycomb: {3[8]}






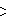

- 7-simplex honeycomb: {3[8]}
- 135 uniquely ringed forms, including:
- Regular 7-cube honeycomb: {4,34,4} = {4,34,31,1},












 =
= 













- Regular 7-cube honeycomb: {4,34,4} = {4,34,31,1},
- 191 uniquely ringed forms, 127 shared with , and 64 new, including:
- 7-demicube honeycomb: h{4,34,4} = {31,1,34,4},












 =
= 











- 7-demicube honeycomb: h{4,34,4} = {31,1,34,4},
- , [31,1,33,31,1]: 77 unique ring permutations, and 10 are new, the first Coxeter called a quarter 7-cubic honeycomb.







 ,
, 







 ,
, 







 ,
, 







 ,
, 







 ,
, 







 ,
, 







 ,
, 







 ,
, 







 ,
, 







- 143 uniquely ringed forms, including:
- 133 honeycomb: {3,33,3},








- 331 honeycomb: {3,3,3,33,1},







- 133 honeycomb: {3,33,3},
Regular and uniform hyperbolic honeycombs
There are no compact hyperbolic Coxeter groups of rank 8, groups that can generate honeycombs with all finite facets, and a finite vertex figure. However, there are 4 paracompact hyperbolic Coxeter groups of rank 8, each generating uniform honeycombs in 7-space as permutations of rings of the Coxeter diagrams.
| = [3,3[7]]: |
= [31,1,32,32,1]: |
= [4,33,32,1]: |
= [33,2,2]: |
References
- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- A. Boole Stott: Geometrical deduction of semiregular from regular polytopes and space fillings, Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910
- H.S.M. Coxeter:
- H.S.M. Coxeter, M.S. Longuet-Higgins und J.C.P. Miller: Uniform Polyhedra, Philosophical Transactions of the Royal Society of London, Londne, 1954
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 Wiley::Kaleidoscopes: Selected Writings of H.S.M. Coxeter
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Klitzing, Richard. "8D uniform polytopes (polyzetta)".